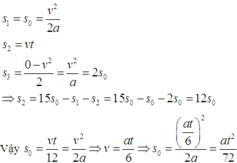chứng minh trong chuyển động thẳng 2 quãng đường trong khoảng thời gian t liên tiếp là 1 hằng số dương nếu chuyển động nhanh dần đều và âm nếu cđ chậm dần đều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng công thức tính đường đi s = 1 2 a t 2 ta được:
s 1 = 1 2 a t 2 ; s 2 = 1 2 a 2 t 2 = 4 2 a t 2 ; s 3 = 1 2 a 3 t 2 = 9 2 a t 2 ... ;
s n − 1 = 1 2 a n − 1 t 2 a t 2 ; s n = 1 2 a n t 2 = n 2 2 a t 2 .
Do đó Δ s 1 = s 1 − 0 = 1 2 a t 2 ; Δ s 2 = s 2 − s 1 = 3 2 a t 2 ; Δ s 3 = s 3 − s 2 = 5 2 a t 2 ... ;
Δ s n = s n − s n − 1 = 1 2 n 2 − n − 1 2 a t 2 = 2 n − 1 2 a t 2 .
Suy ra Δ s 2 Δ s 1 = 3 ; Δ s 3 Δ s 1 = 5 ; ... ; Δ s n Δ s 1 = 2 n − 1 .
Từ đó suy ra Δ s 1 : Δ s 2 : Δ s 3 : ... = 1 : 3 : 5 : ...

Đáp án C
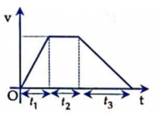
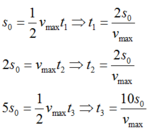
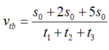
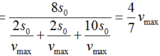
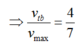
Chú ý: Vật chuyển động gồm ba giai đoạn (như hình vẽ): nhanh dần – đều – chậm dần đều ta có công thức