A=4+4^2+4^3+...+4^100. Tìm số tự nhiên n biết rằng 3.A+4=4n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VG
3
14 tháng 12 2022
A= 3 + 32 + 33 + ... + 3100
3A = 32 + 33 + 34 + ... + 3101
3A - A = (32 + 33 + 34 + ... + 3101) - (3 + 32 + 33 + ... + 3100)
2A = 3101 - 3
Ta có: 2A + 3 = 34n+1
= 3101 - 3 + 1 = 34n+1
= 3101 = 34n+1
=> 4n + 1 =101
4n = 101 - 1
4n = 100
n = 100 : 4
n = 25
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
14 tháng 12 2022
A = 3 + 32 + 33 + 34 +......+ 3100
3A = 32 + 33 + 34+.........+ 3100+ 3101
3A - A = 3101 - 3
2A = 3101 - 3
2A + 3 = 3101 - 3 + 3 = 3101
2A + 3 = 34n+1 ⇔ 3101 = 34n+1
101 = 4n + 1
4n = 101 - 1
4n = 100
n = 100 : 4
n = 25
D
1
NM
Nguyễn Minh Quang
Giáo viên
21 tháng 12 2020
ta có
\(A=3+3^2+..+3^{100}\)
\(\Rightarrow3A=3^2+3^3+..+3^{100}+3^{101}=\left(3+3^2+..+3^{100}\right)+3^{101}-3\)
hay \(3A=A+3^{101}-3\Leftrightarrow2A+3=3^{101}\)
vậy n=101
DT
4
24 tháng 12 2021
3A = 3^2 + 3^3 + 3^4 + ... + 3^101
3A - A = ( 3^2 + 3^3 + 3^4 + .... + 3^101 ) - ( 3 + 3^2 + 3^3 + ... + 3^100 )
2A = 3^101 - 3
Ta có: 2A + 3 = 3^101 = 3^4 . 25 + 1
Vậy, n=25
PT
1
PT
1
CM
9 tháng 9 2018
a, 2 n = 4 ⇒ 2 n = 2 2 ⇒ n = 2
b, 3 n + 1 = 27 = 3 3
⇒ n + 1 = 3 ⇒ n = 2
c, 4 + 4 n = 20
⇒ 4 n = 16 = 4 2 ⇒ n = 2
d, 15 n = 225 = 15 2 ⇒ n = 2
D
6
LC
15 tháng 8 2015
=>3A=32+32+…+3101
=>3A-A=32+33+…+3101-3-32-…-3100
=>2A=3101-3
=>2A+3=3101=3N
=>N=101
Vậy N=101
15 tháng 8 2015
3A = \(3^2+3^3+3^4+...+3^{100}+3^{101}\)
\(\Rightarrow3A-A=\left(3^2+3^3+3^4+...+3^{100}+3^{101}\right)\)- \(\left(3+3^2+3^3+..+3^{100}\right)\)
\(\Rightarrow2A=3^{101}-3\Rightarrow2A+3=3^{101}\)
Vậy n = 101
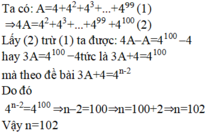
ta có 4. A = 42 + 43 + 44 + ....... + 4101
nên 3.A = 42 + 43 + 44 + ...... +...4101- 4 - 42 - 43 - ......- 4100
3.A = 4101 - 4
=> 3A + 4 = 4101
vậy n = 101
A=4+4^2+4^3+...+4^100
4a-a=4.(4+4^2+4^3+...4^100)-a.(4+4^2+4^3+4^100)
4a=4.4+4.4^2+...+4+4^100-a.4^2...-a.4^100
4a=4^101-4=4^n=n=$^100