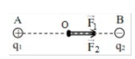
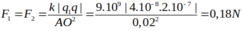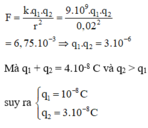Cho 3 điện tích điểm q1 = 4.10-8¬C ; q2 = -4.10-8¬C ; q3 = 5.10-8¬C đặt tại ba đỉnh của một tam giác ABC đều cạnh a = 2cm trong không khí. Xác định vectơ lực tác dụng lên q3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
13 tháng 11 2019
Chọn đáp án D
F = k q 1 q 2 r 2 → Đ ẩ y n h a u q 1 q 2 = F . r 2 k = 6 , 75.10 3 .0 , 02 2 9.10 9 = 3.10 − 16 C q 1 + q 2 = 4.10 − 8 = S q 1 . q 2 = 3.10 − 16 = P ⇒ X 2 − S X + P = 0 ⇔ X 2 − 4.10 − 8 + 3.10 − 16 = 0 ⇒ X = 3.10 − 8 X = 10 − 8
Như vậy ta có hai cặp nghiệm q 1 = 1.10 − 8 C q 2 = 3.10 − 8 C và q 2 = 1.10 − 8 C q 1 = 3.10 − 8 C
Do q 2 > q 1 ⇒ q 2 = 3.10 − 8 C
VT
28 tháng 3 2018
Chọn đáp án A
Muốn vậy điểm C phải nằm trên đường thẳng nối hai điện tích và trong khoảng hai điện tích.
Chọn gốc tọa độ tại A, chiều dương của trục Ox từ A đến B
PT
21 tháng 1 2022
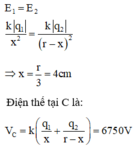
N q1 q2 A E1 E2
Ta có:
\(E_1=\dfrac{9.10^9.4.10^{-8}}{\left(\dfrac{5}{100}\right)^2}=144000\left(v/m\right)\)
\(E_2=\dfrac{9.10^9.4.10^{-8}}{\left(\dfrac{15}{100}\right)^2}=16000\left(v/m\right)\)
\(\Rightarrow E=\left|E_1-E_2\right|=128000\left(v/m\right)\)
Q
6 tháng 8 2021
a, ta để ý CA CB và AB tạo thành tam giác vuông C
\(\Rightarrow E_C=\sqrt{E_A^2+E_B^2}\)
\(E_A=k.\dfrac{\left|4.10^{-8}\right|}{CA^2}=4.10^3\left(V/m\right)\)
\(E_B=k.\dfrac{\left|\dfrac{16}{3}.10^{-8}\right|}{CB^2}=3.10^3\left(V/m\right)\)
\(\Rightarrow E=5000\left(V/m\right)\)
bn nên tập vẽ hình để hiểu hơn nhá
b,\(F_{10}=k.\dfrac{q_1q_0}{CA^2}=4.10^{-3}\left(N\right)\)
\(F_{20}=k.\dfrac{q_2q_0}{CB^2}=3.10^{-3}\left(N\right)\)
\(F=\sqrt{F_{10}^2+F_{20}^2}=5.10^{-3}\left(N\right)\)
VT
29 tháng 6 2018
Đáp án: D
Hai điện tích đẩy nhau = > Cùng dấu =>
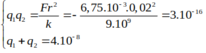
q1 và q2 là nghiệm của phương trình q2 - 4.10-8 + 3.10-16 = 0
=> 
VT
28 tháng 2 2018
Điểm có cường độ điện trường bằng không, tức là:
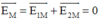
Suy ra: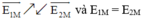 
Do đó điểm này nằm trên đường thẳng nối hai điện tích .
Vì q1 và q2 trái dấu nên điểm này nằm ngoài đoạn thẳng nối hai điện tích và ở về phía gần q1 (vì q1 < | q2 |)
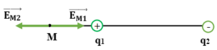
Ta có:
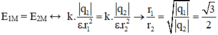
Và r2 – r1 = 10cm (2)
Từ (1) và (2) ta tìm được r1 ≈ 64,6 cm và r2 = 74,6 cm.
Tại điểm đó không có điện trường vì EM = 0.
Đáp số: r1 ≈ 64,64 cm ; r2 ≈ 74,64 cm.
