tìm m để đồ thị hàm số \(y=x^4-2mx^2+2m+m^4\) có 3 điểm cực trị là đỉnh của một tam giác có diện tích bằng 4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 4 2016
Ta có \(y'=4x^3-4mx=4x\left(x^2-m\right);y'=0\Leftrightarrow x=0\) hoặc \(x^2=m\)
Hàm số có 3 điểm cực trị \(\Leftrightarrow\) phương trình \(y'=0\) có 3 nghiệm phân biệt là \(x=0;x=\pm\sqrt{m}\) suy ra đồ thị của hàm số có 3 điểm cực trị là \(A\left(0;m^2-m\right);B\left(-\sqrt{m};-m\right);\overrightarrow{AB}=\left(-\sqrt{m};-m^2\right);\overrightarrow{AC}=\left(\sqrt{m;}-m^2\right)\)
Do đó \(AB=AC=\sqrt{m^4+m}\) nên yêu cầu bài toán được thỏa mãn
\(\Leftrightarrow\widehat{BAC}=120^0\Leftrightarrow\left(\overrightarrow{AB};\overrightarrow{AC}\right)=120^0\)\(\Leftrightarrow\frac{\overrightarrow{AB}\overrightarrow{AC}}{\left|\overrightarrow{AB}\right|\left|\overrightarrow{AC}\right|}=\frac{1}{2}\)
\(\Leftrightarrow\frac{-\left(m\right)+m^4}{m+m^4}=-\frac{1}{2}\Leftrightarrow2m^4-2m=-m-m^4\)
\(\Leftrightarrow3m^4-m=0\Leftrightarrow m\left(3m^3-1\right)=0\Leftrightarrow m=0\) hoặc \(m=\frac{1}{\sqrt[3]{3}}\)
Kết hợp với điều kiện (*) ta có giá trị cần tìm là \(m=\frac{1}{\sqrt[3]{3}}\)
VD
23 tháng 4 2016
Đáp số : \(m=-\frac{1}{\sqrt[3]{3}};m=-\sqrt[3]{\left(2+\sqrt{3}\right)^2}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(y'=4x^3+4\left(m-2\right)x=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=2-m\end{matrix}\right.\)
Hàm có 3 cực trị khi và chỉ khi \(2-m>0\Leftrightarrow m< 2\)
Khi đó gọi 3 cực trị là A, B, C ta có: \(\left\{{}\begin{matrix}A\left(0;m^2-5m+5\right)\\B\left(\sqrt{2-m};1-m\right)\\C\left(-\sqrt{2-m};1-m\right)\end{matrix}\right.\)
Tam giác ABC luôn cân tại A
Gọi H là trung điểm BC \(\Rightarrow H\left(0;1-m\right)\)
\(AH=\left|y_A-y_H\right|=\left|m^2-4m+4\right|=\left(m-2\right)^2\)
\(BC=2\sqrt{2-m}\)
Do ABC đều \(\Rightarrow AH=\dfrac{\sqrt{3}}{2}BC\Leftrightarrow\left(m-2\right)^2=\dfrac{\sqrt{3}}{2}\sqrt{2-m}\)
\(\Leftrightarrow\left(2-m\right)^3=\dfrac{3}{4}\Rightarrow m=2-\sqrt[3]{\dfrac{3}{4}}\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
a. Hàm có 3 cực trị \(\Rightarrow m< 0\)
\(y'=8x^3+4mx=4x\left(2x^2+m\right)=0\Rightarrow\left[{}\begin{matrix}x=0;y=-\dfrac{3m}{2}\\x=-\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\\x=\sqrt{-\dfrac{m}{2}};y=-\dfrac{m^2+3m}{2}\end{matrix}\right.\)
Trong đó \(A\left(0;-\dfrac{3m}{2}\right)\) là cực đại và B, C là 2 cực tiêu
Do tam giác ABC luôn cân tại A \(\Rightarrow\) tâm I của đường tròn ngoại tiếp luôn nằm trên trung trực BC hay luôn nằm trên Oy
Mà tứ giác ABCO nội tiếp \(\Rightarrow OI=AI\Rightarrow I\) là trung điểm OA (do I, O, A thẳng hàng, cùng nằm trên Oy)
\(\Rightarrow I\left(0;-\dfrac{3m}{4}\right)\)
Mặt khác trung điểm BC cũng thuộc Oy và IB=IC (do I là tâm đường tròn ngoại tiếp)
\(\Rightarrow\) I trùng trung điểm BC
\(\Rightarrow-\dfrac{3m}{4}=-\dfrac{m^2+3m}{2}\) \(\Rightarrow m\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2021
b.
Từ câu a ta thấy khoảng cách giữa 2 cực đại là:
\(\left|x_B-x_C\right|=2\sqrt{-\dfrac{m}{2}}=5\Rightarrow m=-\dfrac{25}{2}\)
CM
26 tháng 5 2017
Chọn C
Ta có
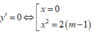nên hàm số có 3 điểm cực trị khi m > 1.
Với đk m > 1 đồ thị hàm số có 3 điểm cực trị là:
Ta có:
Để 3 điểm cực trị của đồ thị hàm số tạo thành tam giác đều thì:
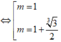
So sánh với điều kiện ta có: m = 1 + 3 3 2 thỏa mãn.
[Phương pháp trắc nghiệm]
Yêu cầu bài toán
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(y'=4mx^3-8x=0\Rightarrow\left[{}\begin{matrix}x=0\\mx^2=2\end{matrix}\right.\)
Hàm có 3 cực trị khi \(m>0\)
Gọi 3 cực trị là A, B, C với \(\left\{{}\begin{matrix}A\left(0;1\right)\\B\left(\sqrt{\dfrac{2}{m}};1-\dfrac{4}{m}\right)\\C\left(-\sqrt{\dfrac{2}{m}};1-\dfrac{4}{m}\right)\end{matrix}\right.\)
Gọi H là trung điểm BC \(\Rightarrow H\left(0;1-\dfrac{4}{m}\right)\)
\(AH=\left|y_A-y_H\right|=\dfrac{4}{m}\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{\dfrac{2}{m}}\)
Tam giác ABC luôn cân tại A nên nó vuông cân khi \(AH=\dfrac{1}{2}BC\)
\(\Leftrightarrow\dfrac{4}{m}=\sqrt{\dfrac{2}{m}}\Rightarrow m=8\)
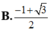
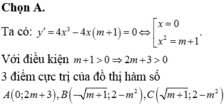
\(y'=4x^3-4mx=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=m\end{matrix}\right.\)
Hàm có 3 cực trị khi \(m>0\)
Gọi 3 cực trị là A; B; C với \(\left\{{}\begin{matrix}A\left(0;m^4+2m\right)\\B\left(\sqrt{m};2m\right)\\C\left(-\sqrt{m};2m\right)\end{matrix}\right.\)
Tam giác ABC luôn cân tại A, gọi H là trung điểm BC \(\Rightarrow H\left(0;2m\right)\)
\(AH=\left|y_A-y_H\right|=m^4\) ; \(BC=\left|x_B-x_C\right|=2\sqrt{m}\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.m^4.2\sqrt{m}=4\)
\(\Leftrightarrow m^9=16\Rightarrow m=\sqrt[3]{2}\)