Hình bình hành ABCD. Có A(2;1); C(6;7); và M(3;2) là điểm thuộc miền của hình bình hành. viết phương trình AD biết khoảng cách từ m đến CD bằng 5 làn khoảng cách từ M đến AB. D thuộc đường thẳng: x+y-11=0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
3 tháng 10 2023
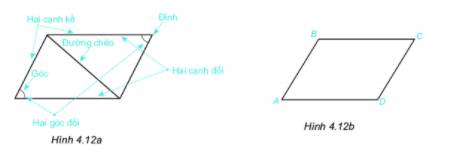
1) Ta đo được: AB = CD; BC = AD. Vậy các cạnh đối của hình bình hành bằng nhau
2) OA = OC; OB = OD
3) + Khi đặt eke vuông góc với AB, ta thấy eke cũng vuông góc với CD. Do đó AB và CD song song với nhau.
+ Khi đặt eke vuông góc với BC, ta thấy eke cũng vuông góc với AD. Do đó BC và AD song song với nhau.
Vậy các cạnh đối của hình bình hành song song với nhau.
4) Gấp giấy, ta thấy các góc đối của hình bình hành bằng nhau.
2 tháng 12 2018
bạn kiếm câu này ở đâu z mình đang luyện thi toán casio mà câu này khó quá bạn có biết chỉ mình
3 tháng 12 2021
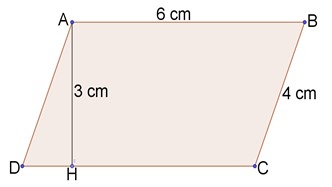
Chiều cao là \(\dfrac{10+10}{2}=10\left(cm\right)\)
Diện tích hbh là \(10\cdot6=60\left(cm^2\right)\)
NT
1
6 tháng 1 2019
hình bình hành ABCD là hình chữ nhật( vì có 1 góc vuông)
Diện tích hình chữ nhật ABCD là
S= AB *AC= 3*5= 15 cm vuông
25 tháng 7 2023
Xét Δ vuông ADC ta có :
\(AD=\dfrac{CD}{2}\)
mà AD là cạnh góc vuông, CD là cạnh huyền
⇒ Δ ADC là tam giác nửa đều
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ADC}=60^O\\\widehat{DCA}=30^O\end{matrix}\right.\)
\(\Rightarrow\widehat{ADC}=\widehat{ABC}=60^O\) (hai góc đối hình bình hành) (1)
Ta lại có : \(\widehat{BAC}=\widehat{DCA}\) (so le trong)
mà \(\widehat{DCA}=30^O\)
\(\Rightarrow\widehat{BAC}=30^2\)
mà \(\widehat{DAB}=\widehat{DAC}+\widehat{BAC}\)
\(\Rightarrow\widehat{DAB}=90^o+30^o=120^o\)
\(\Rightarrow\widehat{BCD}=\widehat{DAB}=120^o\) (hai góc đối hình bình hành) (2)
(1), (2)⇒ điều phải tính toán theo đề