Một con lắc lò xo nằm ngang. Đưa vật đến vị trí lò xo bị nén $12$ cm rồi buông nhẹ, vật dao động điều hòa với chu kỳ T. Thời gian ngắn nhất để tốc độ của vật tăng thêm $30\pi$ (cm/s) kể từ khi buông vật là $\frac{T}{12}$. Hỏi chu kỳ dao động của vật là bao nhiêu?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
6 tháng 10 2018
Đáp án C
Ta có:
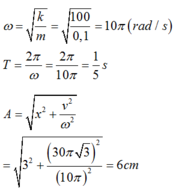
Thời gian tính từ thời điểm ban đầu (x = 30cm, v > 0) đến thời điểm lò xo nén cực đại (x = - 6cm, v = 0) là:
VT
27 tháng 5 2017
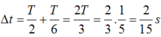
Đáp án C
Ta có : tại thời điểm x = -10 cm vật ở vị trí trên đường tròn số 2 hoặc số 3
Giả sử ta chọn nó đang ở vị trí trên đường tròn số 2 , xét tiếp sau đó khoảng thời gian 3 T 4 ở vị trí đường tròn số 1.
Mà vận tốc v nhanh pha hơn li độ x một góc là π 2
x 1 v à v và v cùng pha ta có : - 10 A = - 100 ω A ⇒ ω = 10 r a d / s
VT
25 tháng 5 2018
Đáp án A
Phương pháp: Sử dụng đường tròn lượng giác và lí thuyết về con lắc lò xo treo thẳng đứng
Cách giải:
- Độ dãn của lò xo khi vật ở vị trí cân bằng:
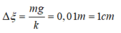
- Kéo vật xuống khỏi vị trí cân bằng theo phương thẳng đứng 2 cm rồi buông nhẹ nên biên độ dao động của vật: A = 2cm.
- Chu kỳ dao động T = 0,2s.
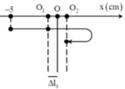
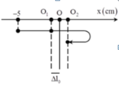
- Lò xo bị nén khi vật di chuyển trong đoạn từ li độ -1cm và biên âm -2cm, được biểu diễn bằng phần tô đậm như hình vẽ.
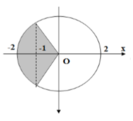
- Trong 0,5s = 2,5T, thời gian lò xo bị nén là: 2T/3 + T/6 = 1,6 (s)
VT
21 tháng 8 2019
Đáp án C
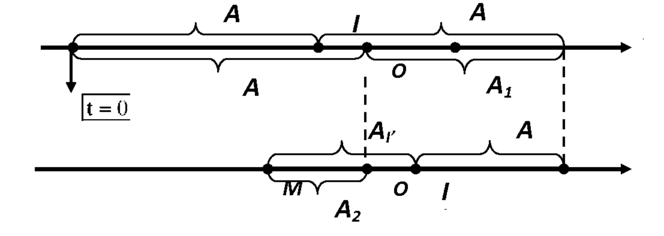
Biên độ còn lại sau mỗi lần qua VTCB O: A 1 = A - 2 x o = 5 - 2 . 1 = 3 c m
*Khi lò xo không biến dạng lần thứ 2 tức là vật đi từ chỗ bị nén ra đến vị trí lò xo giãn nhiều nhất rồi đến vị trí lò xo không biến dạng.
Áp dụng định luật bảo toàn và chuyển hóa cơ năng ta có
VT
16 tháng 7 2019
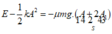
Đáp án D
Độ biến dạng của lò xo tại vị trí cân bằng tạm
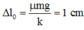
Khi vật đến vị trí lò xo không biến đạng lần 2, quãng đường tương ứng mà vật đã đi được là:
S = 2.4 + 2 = 10cm
Cơ năng lúc này của con lắc bằng hiệu thế năng ban đầu và công của lực ma sát
Ban đầu \(v_0=0\) (cm/s)
Tốc độ của vật tăng thêm \(30\pi\) (cm/s) \(\Rightarrow v_1=30\pi\) (cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian nên ta có thể biểu diễn nó bằng véc tơ quay.
Trong thời gian T/12, góc quay là: \(\alpha=360/12=30^0\)
Ta có:
Ban đầu véc tơ quay ở M ứng với v = 0, lúc sau véc tơ quay đến N.
Ta có: \(30\pi=v_{max}.\sin 30^0\)
\(\Rightarrow v_{max}=60\pi(cm/s)\)
\(\Rightarrow \omega=\dfrac{v_{max}}{A}=5\pi(rad/s)\)
Chu kì: \(T=2\pi/\omega=0,4s\)