Tìm hai số tự nhiên biết rằng ƯCLN của chúng bằng 10, BCNN của chúng bằng 900.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 12 2016
a, Gọi hai số tự nhiên cần tìm là a và b
Ta có : \(a=6.k_1;b=6.k_2\)
Trong đó : \(ƯCLN\left(k_1,k_2\right)=1\)
Mà : \(a+b=84\Rightarrow6.k_1+6.k_2=84\)
\(\Rightarrow6\left(k_1+k_2\right)=84\Rightarrow k_1+k_2=84\div6=14\)
+) Nếu : \(k_1=1\Rightarrow k_2=13\Rightarrow\begin{cases}a=6\\b=78\end{cases}\)
+)Nếu : \(k_1=3\Rightarrow k_2=11\Rightarrow\begin{cases}a=18\\b=66\end{cases}\)
+)Nếu : \(k_1=5\Rightarrow k_2=9\Rightarrow\begin{cases}a=30\\b=54\end{cases}\)
Vậy ...
b, Tương tự câu a,
c, Gọi hai số tự nhiên cần tìm là a và b
Vì : \(ƯCLN\left(a,b\right)=10;BCNN\left(a,b\right)=900\)
\(\RightarrowƯCLN\left(a,b\right).BCNN\left(a,b\right)=a.b=900.10=9000\)
Phần còn lại giống câu a và câu b tự làm
DY
1
6 tháng 11 2016
Gọi các số phải tìm là a và b, giả sử a < b. Ta có ( a, b ) = 10 nên a = 10a', b = 10b', ( a', b' ) = 1, a' < b'. Do đó ab = 100a'b' ( 1 ). Mặt khác ab [ a, b ] . ( a, b ) = 900.10 = 9000 ( 2 )
Từ ( 1 ) và ( 2 ) suy ra a'b' = 90. Ta có các trường hợp
| a' | 1 | 2 | 5 | 9 |
| b' | 90 | 45 | 18 | 10 |
Do đó
| a | 10 | 20 | 50 | 90 |
| b | 900 | 450 | 180 | 100 |
30 tháng 12 2014
a) n=7k+1 ( \(k\in N\))
b) 18 va 66 hoac 6 va 78 hoac 30 va 54
c) 15 va 20 hoac 5 va 60
d) 10 va 900 hoac 20 va 450 hoac 180 va 50 hoac 100 va 90
27 tháng 12 2018
a, Gọi hai số tự nhiên cần tìm là a và b
Ta có : a=6.k1;b=6.k2a=6.k1;b=6.k2
Trong đó : ƯCLN(k1,k2)=1ƯCLN(k1,k2)=1
Mà : a+b=84⇒6.k1+6.k2=84a+b=84⇒6.k1+6.k2=84
⇒6(k1+k2)=84⇒k1+k2=84÷6=14⇒6(k1+k2)=84⇒k1+k2=84÷6=14
+) Nếu : k1=1⇒k2=13⇒{a=6b=78k1=1⇒k2=13⇒{a=6b=78
+)Nếu : k1=3⇒k2=11⇒{a=18b=66k1=3⇒k2=11⇒{a=18b=66
+)Nếu : k1=5⇒k2=9⇒{a=30b=54k1=5⇒k2=9⇒{a=30b=54
Vậy ...
b, Tương tự câu a,
c, Gọi hai số tự nhiên cần tìm là a và b
Vì : ƯCLN(a,b)=10;BCNN(a,b)=900ƯCLN(a,b)=10;BCNN(a,b)=900
⇒ƯCLN(a,b).BCNN(a,b)=a.b=900.10=9000⇒ƯCLN(a,b).BCNN(a,b)=a.b=900.10=9000
Phần còn lại giống câu a và câu b bạn tự làm nha
chúc bạn hok tốt
CM
18 tháng 12 2019
a, Gọi hai số phải tìm là a,b. Ta có (a;b) = 6 => a = 6a’, b = 6b’ với (a’,b’) = 1(a,b,a’,b’ ∈ N)
Do đó: a+b = 84 => 6.(a’+b’) = 84 => a’+b’ = 14
Chọn cặp số a’,b’ là hai số nguyên tố cùng nhau có tổng bằng 14 ta được:
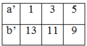
Do đó:
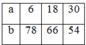
b, Gọi hai số phải tìm là a.b. Ta có (a;b) = 5 => a = 5a’, b = 5b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N)
Do ab = 300 => 25a’b’ = 300 => a’b’ = 12 = 4.3
Chọn cặp số a’,b’ nguyên tố cùng nhau có tích bằng 12 ta được:
a’ = 1, b’ = 12 => a = 5, b = 60
a’ = 3, b’ = 4 => a = 15, b = 20
c, Gọi hai số phải tìm là a,b. Ta có (a;b) = 10 => a = 10a’; b = 10b’ với (a’,b’) = 1 (a,b,a’,b’ ∈ N, a’<b’). Do đó: ab = 100a’b’ (1)
Mặt khác: ab = [a,b].(a,b) = 900.10 = 9000 (2)
a’ = 1, b’ = 90 => a = 10, b = 900
a’ = 2, b’ = 45 => a = 20, b = 450
a’ = 5, b’ = 18 => a = 50, b = 180
a’ = 9, b’ = 10 => a = 90, b = 100
NT
1
10 tháng 4 2016
gọi 2 số đó là a và b ( a < hoặc=b)
Vì ƯCLN của chúng =10=> a=10k b=10q (k,q)=1 (1) (k> hoặc = q)
(vì a.b=Bcnn(a,b). Ư Cln (a,b)=10x900=9000
=> 10k.10q=9000
=>100(k.q)=9000 => k.q=90 (2)
TỪ (1) và (2) => k=10, q=9 hoặc .........
=> a=........ b=..........
Gọi các số phải tìm là a và b, giả sử a < b. Ta có ( a, b ) = 10 nên a = 10a', b = 10b', ( a', b' ) = 1, a' < b'. Do đó ab = 100a'b' ( 1 ). Mặt khác ab [ a, b ] . ( a, b ) = 900.10 = 9000 ( 2 )
Từ ( 1 ) và ( 2 ) suy ra a'b' = 90. Ta có các trường hợp
Do đó
3) Tìm ƯCLN của hai số bằng thuật toán Ơ - clit.