1) đường thẳng xy là đường trung trực của đoạn thẳng AB nếu
a) xy vuông góc AB
b) xy vuông góc với AB hoặc tại A hoặc tại B
c) xy đy qua trung điểm của AB
d) xy vuông góc với AB và đy qua trung điểm của AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 8 2021
Đường thẳng xy là đường trung trực của đoạn thẳng AB thì:
A. Đường thẳng xy vuông góc với đoạn thẳng AB tại I và I là trung điểm của đoạn AB.
B. Đường thẳng xy vuông góc với đoạn thẳng AB.
C. Đường thẳng xy đi qua trung điểm của đoạn thẳng AB
D. Đường thẳng xy vuông góc với đoạn thẳng AB tại A .
11 tháng 8 2021
Ta có : – Góc x’Oy’ và góc xOy là hai góc đối đỉnh ⇒ góc xOy = góc x’Oy’ = 90o
– ∠(xOy) và ∠(xOy’) là hai góc kề bù ⇒ ∠(xOy) + ∠(xOy’) = 180o
⇒ (xOy’) = 180o – (xOy) = 180o– 90o = 90o
– ∠(xOy’) và ∠(x’Oy) là hai góc đối đỉnh ⇒ ∠(xOy’) = ∠(x’Oy) = 90o
Khi đó các góc ∠yOx’ ; ∠x’Oy’ ; ∠y’Ox cũng đều là những góc vuông
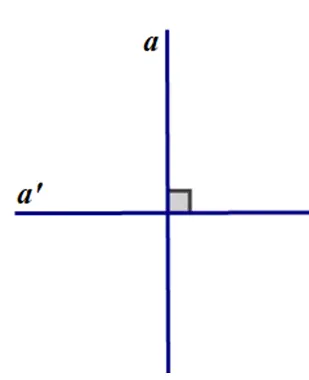
Trả lời câu hỏi Toán 7 Tập 1 Bài 2 trang 84: Vẽ phác hai đường thẳng a và a’ vuông góc với nhau và viết kí hiệu.Lời giải
23 tháng 10 2021
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=5\left(cm\right)\)
b, Vì AI là trung tuyến ứng ch BC nên \(AI=\dfrac{1}{2}BC=2,5\left(cm\right)\)
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{12}{5}=2,4\left(cm\right)\)
10 tháng 12 2016
a) Xét ∆BAD và ∆ACE có:
^BDA=^AEC (cùng bằng 90 độ)
AB=AC (gt)
^BAD=^ACE (cùng phụ với ^EAC)
suy ra ∆BAD=∆ACE (cạnh huyền-góc nhọn)
b) Do ∆BAD=∆ACE nên AD=CE và AE=BD
mà DE=DA+AE
suy ra DE = CE+BD (đpcm)
10 tháng 12 2016
b) Có: BAP + PAC = 90o
t/g BPA vuông tại P có: ABP + BAP = 90o
Suy ra PAC = ABP
Xét t/g BPA vuông tại P và t/g AQC vuông tại Q có:
AB = AC (gt)
ABP = CAQ (cmt)
Do đó, t/g BPA = t/g AQC ( cạnh huyền - góc nhọn)
=> AP = QC (2 cạnh tương ứng)
và BP = AQ (2 cạnh tương ứng)
= AP + PQ = QC + PQ
=> PQ = BP - QC (đpcm)
1) đường thẳng xy là đường trung trực của đoạn thẳng AB nếu
a) xy vuông góc AB
b) xy vuông góc với AB hoặc tại A hoặc tại B
c) xy đy qua trung điểm của AB
d) xy vuông góc với AB và đi qua trung điểm của AB
1) đường thẳng xy là đường trung trực của đoạn thẳng AB nếu
a) xy vuông góc AB
b) xy vuông góc với AB hoặc tại A hoặc tại B
c) xy đy qua trung điểm của AB
d) xy vuông góc với AB và đy qua trung điểm của AB