Bỏ 100g nước đá ở t1= O0C vào 300g nước ở t2= 20oC.
a) Nước đá có tan hết không ? Cho nhiệt nóng chảy của nước đá l= 3,4.105 J/kg và nhiệt dung riêng của nước là c=4200J/kg.k.
b) Nếu không ,tính khối lượng nước đá còn lại ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án : B
- Nhiệt lượng nước đá thu vào để nóng chảy(tan) hoàn toàn ở 0 0 C .
![]()
- Nhiệt lượng nước tỏa ra khi giảm từ 20 0 C đến 0 0 C :
![]()
- Ta thấy Q 1 > Q 2 nên nước đá chỉ tan một phần .

Đáp án : D
- Nhiệt lượng nước đá thu vào để nóng chảy(tan) hoàn toàn ở 0 0 C .
![]()
- Nhiệt lượng nước tỏa ra khi giảm từ 20 0 C đến 0 0 C :
![]()
- Ta thấy Q 1 > Q 2 nên nước đá chỉ tan một phần .
- Nhiệt lượng nước tỏa ra chỉ làm tan một khối lượng Δm nước đá. Do đó :
Q 2 = ∆ m . λ
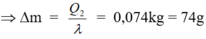
- Vậy nước đá còn lại : m ' = m 1 - ∆ m = 26 g

a, đổi \(100g=0,1kg\),\(300g=0,3kg\)
\(=>Qthu\)(tan chảy đá)\(=0,1.3,4.10^5=34000\left(J\right)\)
\(=>Qtoa\left(nuoc\right)=0,3.4200.20=25200\left(J\right)\)
\(=>Qtoa\left(nuoc\right)< Qthu\)(tan chảy đá) do đó nhiệt lượng tỏa ra chưa đủ làm tan hết đá nên nước đá không tan hết
c, gọi khối lượng nước bổ sung thêm là m1(kg)
=>khối lượng nước thực tế là 0,3+m1(kg)
\(=>34000=\left(0,3+m\right)4200.20=>m\approx0,105kg\)
vậy........

200g=0,2kg
50g=0,05kg
100g=0,1kg
ta có phương trình cân bằng nhiệt:
Qtỏa=Qthu
\(\Leftrightarrow Q=m_1C_1\left(0--10\right)+m_1\lambda+m_1C_2\left(100-0\right)+m_1L\)
\(\Leftrightarrow Q=3600+68000+84000+460000\)
\(\Leftrightarrow Q=615600J\)
nếu bỏ cục nước đá vào nước thì phương trình cân bằng nhiệt là:
Qtỏa=Qthu
\(\Leftrightarrow Q_n+Q_{nh}=Q_{nđ}\)
\(\Leftrightarrow Q_2+Q_3=Q_1\)
\(\Leftrightarrow m_2C_2\left(t_2-t\right)+m_3C_3\left(t_3-t\right)=m_1C_1\left(t-t_1\right)+\left(m_1-0,05\right)\lambda\)
\(\Leftrightarrow4200m_2\left(20-0\right)+88\left(20-0\right)=360\left(0--10\right)+3,4.10^5\left(0,2-0,05\right)\)
\(\Leftrightarrow84000m_2+1760=54600\)
\(\Rightarrow m_2=0,63kg\)
chú ý ở câu b:
nhiệt độ cân bằng là 0 vì nước đá chưa tan hết.
khối lượng nhân cho lamđa phải trừ đi cho phần chưa tan hết
chúc bạn thành công nhé![]()

Đáp án: B
- Nhiệt lượng do cốc và nước toả ra để hạ nhiệt độ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của khối nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Vì Q 1 > Q 2 nên khối nước đá đã tan hết và nhiệt độ hỗn hợp lớn hơn 0 0 C

a, Nhiệt lượng thau nhôm tỏa ra khi hạ từ 20°C đến \(0^oC\) là
\(Q_1=880.0,3.20=5280\left(J\right)\)
Nhiệt lượng nước nhôm tỏa ra khi hạ từ 20°C đến \(0^oC\) là
\(Q_2=4200.0,5.20=42000\) ( J )
Nhiệt lượng cần thiết để nước đá tăng từ -200°C đến \(0^oC\) là
\(Q_3=2100.0,2.200=84000\) ( J )
Nhiệt lượng cần thiết để làm tan 0,2 kg nước đá là
\(Q_4=3,4.10^5.0,2=68000\left(J\right)\)
Ta thấy \(Q_1+Q_2< Q_3+Q_{\text{4}}\) nên nước đá không tan hết
b, Vì \(Q_1+Q_2< Q_3\) nên nước đá chưa bắt đầu tan.
0,5 kg nước cũng sẽ biến thành đá. Nhiệt độ cân bằng bé hơn 0
=)))) Đến đây thì mình chịu. Có lẽ nước đá chỉ ở tầm -20°C thôi. lúc đó nước đá tan đi một it. chứ đề này thấy sai sai
Gọi nhiệt lượng của nước là \(Q_t\) từ \(20^oC\) về \(0^oC\) và của nước đá tan hết là \(Q_{thu}\), ta có:
\(Q_t=m_2c_2.\left(20-0\right)=0,3.4200.20=25200J\)
\(Q_{thu}=m_1.\lambda=0,1.3,4.10^5=34000J\)
Ta thấy Qthu > Qtỏa nên nước đá không tan hết. Lượng nước đá chưa tan hết là:
\(m=\frac{Q_{thu}-Q_{tỏa}}{\lambda}\)\(=\frac{8800}{3,4.10^5}=0,026\left(kg\right)\)