Gắn lần lượt hai quả cầu có khối lượng m1 và m2 vào một lò xo và cho chúng dao động. Trong cùng một khoảng thời gian, quả cầu m1 thực hiện 10 dao động còn quả cầu m2 thực hiện được 5 dao động. So sánh m1 và m2?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 7 2016
1. Chu kì 2 vật là:
\(T_1=2\pi\sqrt{\dfrac{m_1}{k_1}}\)
\(T_2=2\pi\sqrt{\dfrac{m_2}{k_2}}\)
Có \(T_1=T_2\)
\(\Rightarrow \dfrac{m_1}{k_1}=\dfrac{m_2}{k_2}\)
\(\Rightarrow \dfrac{k_2}{k_1}=\dfrac{m_2}{m_1}=3\)
Mà với 1 lò xo thì \(k.l=const\)
\(\Rightarrow k_1.l_1=k_2.l_2\)
\(\Rightarrow k_1.CA=k_2.CB\)
\(\Rightarrow \dfrac{k_2}{k_1}=\dfrac{CA}{CB}=3\)
\(\Rightarrow \dfrac{CA}{CA+CB}=\dfrac{3}{3+1}\)
\(\Rightarrow \dfrac{CA}{AB}=\dfrac{3}{4}\)
16 tháng 7 2016
Tần số dao động:
\(f_1=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m_1}}\)
\(f_2=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m_2}}\)
Ta có: \(\dfrac{f_1}{f_2}=\sqrt{\dfrac{m_2}{m_1}}=\dfrac{10}{5}=2\)
\(\Rightarrow \dfrac{m_1}{m_2}=4\)
Nếu treo cả 2 quả cầu vào lò xo thì chu kì là: \(T=2\pi\sqrt{\dfrac{m_1+m_2}{k}}=2\pi\sqrt{\dfrac{m_1+\dfrac{m_1}{4}}{96}}=\dfrac{\pi}{2}\)
\(\Rightarrow m_1 = 4,8kg\)
VT
19 tháng 5 2018
Đáp án B
Phương pháp: Chu ki dao đông̣ điều hoa cua con lắc lo xo T = 2 π m k
Cách giải:
Theo bài ra ta có
HD
Hà Đức Thọ
Admin
24 tháng 8 2015
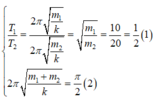
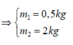
Ta có: \(t=20T_1=10T_2\Rightarrow\frac{T_1}{T_2}=\frac{1}{2}\)
\(\Rightarrow\sqrt{\frac{m_1}{m_2}}=\frac{1}{2}\Rightarrow\frac{m_1}{m_2}=\frac{1}{4}\)(1)
Treo đồng thời 2 vật vào lò xo thì chu kì: \(T=2\pi\sqrt{\frac{m_1+m_2}{k}}=\frac{\pi}{2}\Leftrightarrow m_1+m_2=2,5\)kg (2)
Từ (1) và (2) suy ra: \(\begin{cases}m_1=0,5kg\\m_2=2kg\end{cases}\)
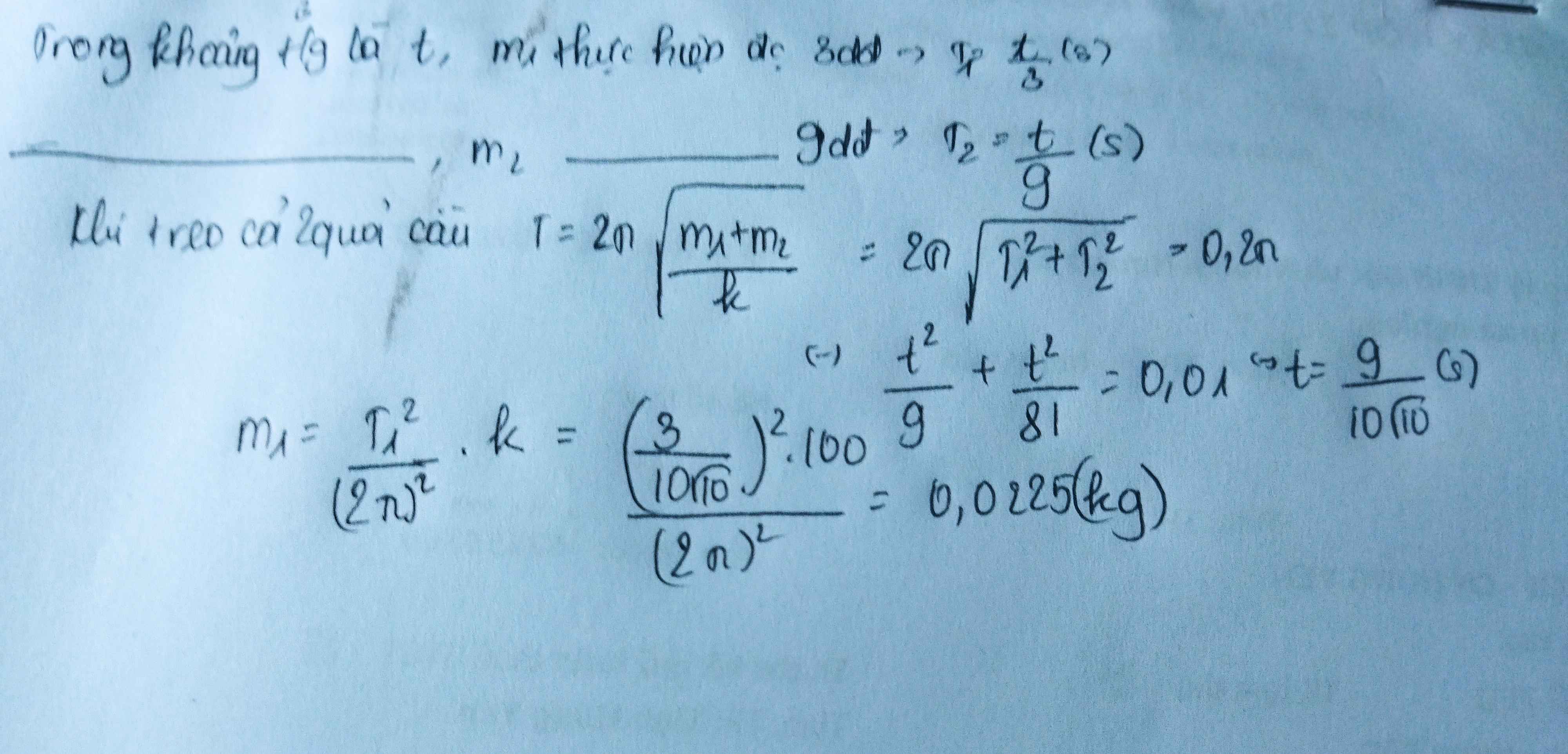
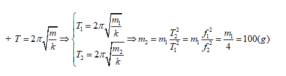
Trong một khoảng thời gian là t, m1 thực hiện được 10 dao động=> T1=t/10 (s)
Trong một khoảng thời gian là t, m2 thực hiện được 5 dao động=> T2=t/5 (s)
Có khối lượng luôn tỉ lệ thuận với bình phương chu kỳ của vật đó => vật có chu kỳ càng lớn thì khối lượng càng lớn. Ta lại có T1<T2=> m1<m2