Cho góc nhọn xOy, trên tia Ox lấy điểm A ( A \(\notin\) O) , trên tia Oy lấy điểm B ( B \(\notin\) O ) sao cho OA=OB; kẻ AC vông góc với Oy ( C \(\in\) Oy); BD vuông góc với Ox ( D \(\in\) Ox ); I là giao điểm của AC và BD
a) Chứng minh tam giác AOC = tam giác BOD
b) Chứng minh tam giác AIB cân
c) So sánh IC và IA
d) Chứng minh góc IAB= 1/2 AOB
(cứu mình với ạ , ai biết làm xin giải giúp )

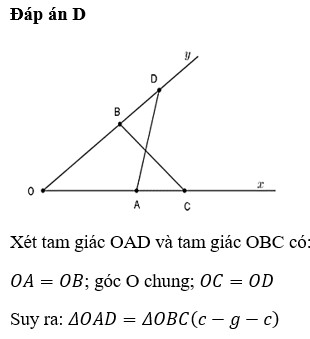
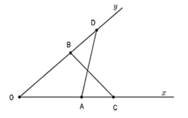




Bạn tự vẽ hình nha
a.
Xét tam giác COA vuông tại C và tam giác DOB vuông tại D có:
OA = OB (gt)
AOB là góc chung
=> Tam giác COA = Tam giác DOB (cạnh huyền - góc nhọn)
b.
OA = OB (gt)
=> Tam giác OAB cân tại O
OAC + CAB = OAB
OBD + DBA = OBA
mà OAC = OBD (tam giác AOC = tam giác BOD)
OAB = OBA (tam giác OAB cân tại O)
=> CAB = DBA
=> Tam giác IAB cân tại I
c.
Tam giác CIB vuông tại C có:
IC < IB (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà IA = IB (tam giác IBA cân tại I)
=> IC < IA
d.
Tam giác OAB cân tại O
=> \(OBA=\frac{180-AOB}{2}=\frac{180}{2}-\frac{AOB}{2}=90-\frac{AOB}{2}\)
Tam giác CAB vuông tại C có:
IAB + OBA = 90
IAB = 90 - OBA = \(90-\left(90-\frac{AOB}{2}\right)=90-90+\frac{AOB}{2}=\frac{AOB}{2}\)
=> IAB = 1/2 AOB
Chúc bạn học tốt