Cho hình chóp SABC. gọi N là điểm nằm trên cạnh SB. M , P là điểm thuộc miền trong mặt phẳng ( SAB ) và (SBC). Tìm thiết diện tạo bởi (MNP) và hình chóp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
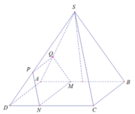
Trong mặt phẳng (ABCD) kẻ Mx song song với BC
Mx cắt CD tại N
⇒ MN // (SBC) (1)
Trong mặt phẳng (SCD) kẻ Ny song song với SC
Ny cắt SD tại P
⇒ NP // (SBC) (2)
Trong mặt phẳng (SAB) kẻ Mz song song với SB
Mz cắt SA tại Q
⇒ MQ // (SBC) (3)
Từ (1), (2), (3), ta có thiết diện MNPQ tạo bởi mặt phẳng (P) và hình chóp SABCD
Xét tứ diện MNPQ có:
A M A B = D N D C = A Q A S = D P D S
⇒ PQ // AD ⇒ PQ // MN
⇒ MNPQ là hình thang

a/ \(\left\{{}\begin{matrix}S=\left(SAB\right)\cap\left(SCD\right)\\Sx//AB//CD\end{matrix}\right.\Rightarrow\left(SAB\right)\cap\left(SCD\right)=Sx\)
b/ \(\left(MCD\right)\cap\left(ABCD\right)=CD\)
\(\left(MCD\right)\cap\left(SBC\right)=MC\)
\(\left(MCD\right)\cap\left(SCD\right)=CD\)
\(\left(MCD\right)\cap\left(SAB\right)=My\left(My//AB//CD\right)\)
\(\Rightarrow TD:CDM\)
Vậy thiết diện là hình tam giác.
P/s: Chắc bạn sẽ thắc mắc tại sao lại ko xét trường hợp (MCD) cắt (SAD). Bởi vì chúng ko có giao tuyến :)
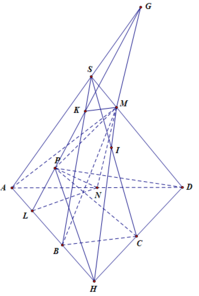


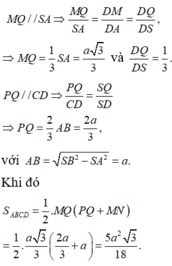


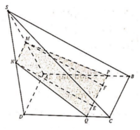
À, "không tính" là đang nói tới D, E trong hình vẽ của em (nằm trên cạnh chóp kéo dài), không phải D, E trong hình của mình (nằm trên cạnh chóp)