Tìm k để PT : -x3 +3x2 + k3 - 3k2 =0 có 3 nghiệm phân biệt
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Xét hàm số f x = x 3 − 3 x 2 + 1 có:
f ' x = 3 x 2 − 6 x = 3 x x − 2 ⇒ f ' x = 0 ⇔ x = 0 x = 2
Ta có bảng biến thiên của như sau:
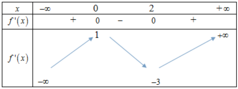
Từ bảng biến thiên này ta có bang biến thiên của f x = x 3 − 3 x + 1 như sau:
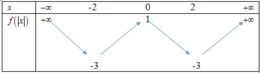
Dựa trên bảng biến thiên này ta thấy PT:
x 3 − 3 x 2 + 1 - m = 0 ⇔ x 3 − 3 x 2 + 1 = m có 4 nghiệm phân biệt ⇔ − 3 < m < 1

Đáp án D
· Điều kiện cần:
Giả sử phương trình đã cho có 3 nghiệm phân biệt x 1 ; x 2 ; x 3 lập thành một cấp số cộng
Khi đó: x 1 + x 3 = 2 x 2 x 1 + x 2 + x 3 = 3 ⇔ 3 x 2 = 3 ⇔ x 2 = 1 .
Với x 2 = 1 thay vào phương trình ta được:
1 − 3 + m + 2 − m = 0 (luôn đúng).
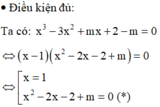
Phương trình đã cho có 3 nghiệm phân biệt tương đương với phương trình (*) có 2 nghiệm phân biệt khác 1.
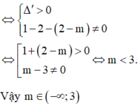

\(x^3-x^2+2mx-2m=0\)
\(\Leftrightarrow x^2\left(x-1\right)+2m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+2m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2=-2m\end{matrix}\right.\)
Để pt có 3 nghiệm \(\Rightarrow-2m>0\Rightarrow m< 0\)
a. Do vai trò 3 nghiệm như nhau, ko mất tính tổng quát giả sử \(x_1=1\) và \(x_2;x_3\) là nghiệm của \(x^2+2m=0\)
Để pt có 3 nghiệm pb \(\Rightarrow\left\{{}\begin{matrix}-2m>0\\-2m\ne1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< 0\\m\ne-\dfrac{1}{2}\end{matrix}\right.\)
Khi đó: \(x_2+x_3=0\Rightarrow x_1+x_2+x_3=1\ne10\) với mọi m
\(\Rightarrow\) Không tồn tại m thỏa mãn yêu cầu
b.
Giả sử pt có 3 nghiệm, khi đó \(\left[{}\begin{matrix}x_2=-\sqrt{-2m}< 0< 1\\x_3=\sqrt{-2m}\end{matrix}\right.\)
\(\Rightarrow\) Luôn có 1 nghiệm của pt âm \(\Rightarrow\) không tồn tại m thỏa mãn
Em coi lại đề bài

Chọn B.
Điều cần cần:
Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng.
Khi đó: x 1 + x 3 = 2 x 2 ,
Lại có :
x 1 + x 2 + x 3 = − b a = 3 ⇒ x 2 = 1
Thay vào phương trình ta được: 13 – 3.12 – 9.1 + m =0
⇔ m = 11
* Điều kiện đủ : Với m =11 phương trình trở thành :
x 3 − 3 x 2 − 9 x + 11 = 0
⇔ x − 1 x 2 − 2 x − 11 = 0 ⇔ x 1 = 1 − 12 , x 2 = 1, x 3 = 1 + 12
Ba nghiệm này lập thành cấp số cộng.
Vậy m =11 là giá trị cần tìm.

Lời giải:
$\Delta'=4-6m$
a. Để pt có nghiệm thì $\Delta'=4-6m\geq 0\Leftrightarrow m\leq \frac{2}{3}$
b/ Để pt có 2 nghiệm phân biệt thì $\Delta'=4-6m>0\Leftrightarrow m< \frac{2}{3}$
c. Để pt có nghiệm kép thì $\Delta'=4-6m=0\Leftrightarrow m=\frac{2}{3}$
d. Để pt vô nghiệm thì $\Delta'=4-6m< 0\Leftrightarrow m> \frac{2}{3}$
a: \(\text{Δ}=\left(-4\right)^2-4\cdot3\cdot2m=-24m+16\)
Để phương trình có nghiệm thì \(\text{Δ}\ge0\)
\(\Leftrightarrow-24m+16\ge0\)
\(\Leftrightarrow-24m\ge-16\)
hay \(m\le\dfrac{2}{3}\)
b: Để phương trình có hai nghiệm phân biệt thì Δ>0
hay \(m< \dfrac{2}{3}\)
c: Để phương trình có nghiệm kép thì Δ=0
hay \(m=\dfrac{2}{3}\)

Đáp án A
Điều kiện cần: Giả sử phương trình có ba nghiệm phân biệt lập thành cấp số cộng, khi đó
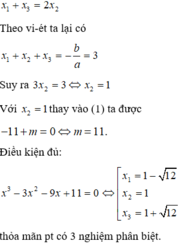

Đáp án B
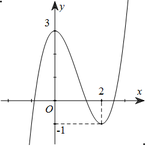
Phương trình đã cho ⇔ x 3 + 3 x 2 − 9 x = − m
Lập bảng biến thiên hàm số y = x 3 + 3 x 2 − 9 x
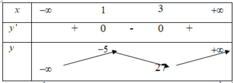
Để phương trình ban đầu có 3 nghiệm phân biệt thì đường thẳng y = − m cắt đồ thị hàm số y = x 3 + 3 x 2 − 9 x tại 3 điểm phân biệt ⇔ − 5 < − m < 27 ⇔ − 27 < m < 5


pt tương đương vs (x-k)(x^2+xk+k^2)=3(x-k)(x+k)
vậy chắc chắn có 1 nghiệm là x=k. để pt có 3 nghiệm phân biệt thì pt x^2+kx+k^2=3(x+k) phải có 2 nghiệm phân biệt khác k.
pt này có đenta= (k-3)^2-4(k^2-3k)=6k+9-3k^2.
đenta phải dương=> 0>3k^2-9k-6 hay 0>3(k+1)(k-3) => 3>k>-1.
khi đó 2 nghiệm pt là (3-k+căn đenta):2 và (3-k-căn đenta):2.
pt tương đương vs (x-k)(x^2+xk+k^2)=3(x-k)(x+k)
vậy chắc chắn có 1 nghiệm là x=k. để pt có 3 nghiệm phân biệt thì pt x^2+kx+k^2=3(x+k) phải có 2 nghiệm phân biệt khác k.
pt này có đenta= (k-3)^2-4(k^2-3k)=6k+9-3k^2.
đenta phải dương=> 0>3k^2-9k-6 hay 0>3(k+1)(k-3) => 3>k>-1.
khi đó 2 nghiệm pt là (3-k+căn đenta):2 và (3-k-căn đenta):2.