Cho mik hỏi trực tâm có đc gọi là trọng tâm hk
Thanks mí bạn nhìu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 4 2019
H O G A B M C k
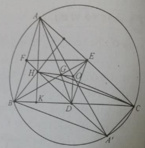
Ây za cách này khá là cùi bắp nhưng mà em tham khảo nhé:
Lấy điểm K đối xứng với C qua O
Xét tam giác CKB có: O là trung điểm CK , M là trung điểm BC
C K B O M N
Gọi N là điểm đối xứng với O qua M
Tam giác OCM=tam giác NBM
=> OC//BN
OC=BN
Tam giác OBN = tam giác BOK (1)
=> ON=KB
mà OM=1/2ON
=> OM=1/2KB
Từ (1) suy ra đc OM//KB
mà OM//AH ( cùng vuông Bc)
=> KB//AH (3)
Chứng minh tương tự => BH//KA (4)
Từ (3), (4) chứng minh đc tam giác KBA=HAB
=> KB=HA
=> OM=1/2 AH
Sử dụng định lí Ta let
OM//AH=> \(\frac{GM}{AG}=\frac{OM}{AH}=\frac{1}{2}\)
mà AM là đường trung tuyến
=> G là trọng tâm.
CM
15 tháng 11 2017
G D → = - 1 / 2 G A → ⇒ phép vị tự tâm G tỉ số -1/2 biến A thành D.
Đáp án B.
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2022
Do \(SO\perp ABC\Rightarrow\) các tam giác SOA, SOB, SOC đều vuông tại O
Đặt \(SA=SB=SC=a\) , áp dụng Pitago:
\(OA=\sqrt{SA^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OB=\sqrt{SB^2-SO^2}=\sqrt{a^2-SO^2}\)
\(OC=\sqrt{SC^2-SO^2}=\sqrt{a^2-SO^2}\)
\(\Rightarrow OA=OB=OC\Rightarrow O\) là tâm đường tròn ngoại tiếp tam giác ABC
CM
12 tháng 7 2017
Gọi A’ là điểm đối xứng với A qua tâm O.
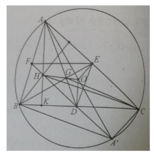
chứng minh BHCA’ là hình bình hành, suy ra H, A', D thẳng hàng và DO là đường trung bình của tam giác AHA’ ⇒ D O → = - 1 / 2 A H → ⇒ phép vị tự tâm G tỉ số -1/2 biến A H → thành DO → .
Đáp án B
16 tháng 3 2020
a,+) Lấy N sao cho : O là trung điểm của CN ; lấy M sao cho : OM là trung trực của BC
\(\implies\) OM là đường trung bình của tam giác CNB
\(\implies\) OM song song với NB ; OM = \(\frac{1}{2}\) NB
Ta có : OM vuông góc với BC \(\implies\) NB vuông góc với BC mà AH vuông góc với BC
\(\implies\) NB song song với AH ( 1 )
+) Lấy S sao cho : OS là trung trực của AC ; mà O là trung điểm của NC
\(\implies\) OS là đường trung bình của tam giác NAC
\(\implies\) OS song song với AN ; OS = \(\frac{1}{2}\) AN
Ta có : OS vuông góc với AC \(\implies\) NA vuông góc với AC mà BH vuông góc với AC
\(\implies\) NA song song với BH ( 2 )
Từ ( 1 ) ; ( 2 )
\(\implies\) NAHB là hình bình hành
\(\implies\) NB = AH ( 3 )
Mà OM = \(\frac{1}{2}\) NB \(\implies\) 2OM = NB ( 4 )
Từ ( 3 ) ; ( 4 )
\(\implies\) AH = 2OM ( đpcm )
b, Ta có : A ; G ; M thẳng hàng ( M là trung điểm của BC ; G là trọng tâm )
GM = \(\frac{1}{3}\) AM \(\implies\) AG = 2GM
Gọi I ; K lần lượt là trung điểm của HG ; AG
\(\implies\) IK là đường trung bình của tam giác HGA
\(\implies\) IK song song với AH ; IK = \(\frac{1}{2}\) AH
+) NB song song OM , mà NB song song với AH
\(\implies\) AH song song với OM
+) AH song song với OM , mà IK song song với AH
\(\implies\) IK song song với OM
\(\implies\) IKG = GMO ( 2 góc so le trong )
+) IK = \(\frac{1}{2}\) AH , mà AH = 2OM
\(\implies\) IK = OM
+) K là trung điểm của AG
\(\implies\) KA = KG = \(\frac{AG}{2}\)
Mà AG = 2GM \(\implies\) KA = KG = GM \(\implies\) KG = GM
+)Xét tam giác KIG và tam giác MOG có :
KG = GM
IKG = GMO ( cmt )
OM = KI
\(\implies\) tam giác KIG = tam giác MOG ( c - g - c )
\(\implies\) IGK = OGM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí 2 góc đối đỉnh
\(\implies\) I , G , O thẳng hàng
\(\implies\) H , G , O thẳng hàng
+) I là trung điểm của HG
\(\implies\) IH = IG = \(\frac{HG}{2}\)
\(\implies\) 2IH = 2IG = HG ( 5 )
+) IG = GO ( tam giác KIG = tam giác MOG )
\(\implies\) 2IG = 2GO ( 6 )
Từ ( 5 ) ; ( 6 )
\(\implies\) HG = 2GO
16 tháng 3 2020
Trong một tam giác :
+)3 đường trung tuyến đồng quy : trọng tâm
+)3 đường phân giác đồng quy : tâm đường tròn nội tiếp tam giác
+)3 đường cao đồng quy : trực tâm
+)3 đường trung trực đồng quy : tâm đường tròn ngoại tiếp tam giác
28 tháng 4 2016
a, Trọng tâm của tam giác cách đỉnh 2/3 đường trung tuyến đi qua đỉnh ấy
Cánh xác định trọng tâm: vẽ 2 đường trung tuyến của tam giác, 2 đường đó cắt nhau tại điểm nào thì đó là trọng tâm của tam giác
b, Bạn Nam nói sai. Vì 3 đường trung tuyến của tam giác luôn ở trong tam giác nên giao điểm của chúng hay trọng tâm của tam giác luôn ở trong tam giác
BT
28 tháng 4 2016
Tính chất:
Trọng tâm cách đỉnh một khoảng bằng hai phần ba đường trung tuyến đi qua đỉnh ấy.
Cách xác định trọng tâm:
Trọng tâm là giao điểm của 3 đường trung tuyến của tam giác.
Đường trung tuyến của tam giác là đường thẳng hạ từ đỉnh tới trung điểm của cạnh đối diện.
Nói vậy chắc bạn cũng hiểu rồi, cách vẽ trong SGK đó nhé.
b) Nam nói sai. Vì trọng tâm cách đỉnh bằng 2 phần 3 đường trung tuyến đi qua đỉnh nên khoảng cách từ trọng tâm đến đỉnh luôn nhỏ hơn khoảng cách từ đỉnh đó đến trung điểm của cạnh đối diện.
Phù!!! Cuối cùng cũng xong, k nhé.
Trực tâm và trọng tâm hoàn toàn khác nhau bạn nhé!
Đoạn thẳng nối một đỉnh với hình chiếu vuông góc của nó trên cạnh đối diện được gọi là đường cao của tam giác. Một tam giác có ba đường cao. Ba đường cao của một tam giác cắt nhau tại một điểm, điểm này được gọi là trực tâm của tam giác.
Đoạn thẳng nối mỗi đỉnh với trung điểm của cạnh đối diện được gọi là trung tuyến của tam giác, một tam giác có ba đường trung tuyến. Ba đường trung tuyến của một tam giác cắt nhau tại một điểm, điểm này được gọi là trọng tâm của tam giác.
Chúc bạn học tốt!
trực tâm không được gọi là trong tâm. ( trừ một số trường hợp đặc biệt như tâm giác đều....)
Trong sản xuất nông nghiệp các hoạt động kinh tế làm cho độ phì của đất tăng hoặc giảm:
-Trọng tâm tam giác là giao điểm ba đường trung tuyến
-Trực tâm tam giác là giao điểm bà đường cao kẻ từ 3 đỉnh tam giác
về khái niệm nó đã khác hẳn nhau rồi thì làm sao mà như nhau được.