Cho hàm số \(y=x^3-2x^2+\left(1-m\right)x+m\left(1\right)\), m là số thực. Tìm m để đồ thị hàm số (1) cắt trục hoành tại 3 điểm phân biệt có hoành độ \(x_1;x_2;x_3\) thỏa mãn điều kiện \(x_1^2+x^2_2+x^2_3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
31 tháng 8 2023
(d) cắt trục hoành độ là 1:
⇒ \(x=1\)
Và hàm số: \(y=0\)
Thay \(x=1\) tại giá trị hàm số \(y=0\)
Ta có:
\(y=\left(m-3\right)\cdot1+3m-1=0\)
\(\Leftrightarrow\left(m-3\right)+3m-1=0\)
\(\Leftrightarrow m-3+3m-1=0\)
\(\Leftrightarrow4m-4=0\)
\(\Leftrightarrow4m=4\)
\(\Leftrightarrow m=1\)
Vậy: ...
30 tháng 8 2023
3: Thay x=1 và y=0 vào (d), ta được:
m-3+3m-1=0
=>4m-4=0
=>m=1
21 tháng 4 2016
Phương trình hoành độ giao điểm : \(-x^4+2\left(2+m\right)x^2-3-2m=0\left(1\right)\)
Đặt \(t=x^2,\left(t\ge0\right)\), phương trình (1) trở thành : \(t^2-1\left(m+2\right)t+3+2m=0\left(2\right)\)
(1) có 4 nghiệm phân biệt khi và chỉ khi (2) có 2 nghiệm dương phân biệt
Điều kiện là : \(\begin{cases}\Delta'>0\\S>0\\P>0\end{cases}\) \(\Leftrightarrow\begin{cases}m^2+2m+1>0\\m+2>0\\3+2>0\end{cases}\) \(\Leftrightarrow\begin{cases}m\ne-1\\m>-\frac{3}{2}\end{cases}\) (*)
Với điều kiện (*), giả sử \(t_1;t_2\) (\(0 < t 1 < t2 \) là 2 nghiệm phân biệt của (2), khi đó (1) có 4 nghiệm phân biệt là \(x_1=-\sqrt{t_2};x_2=-\sqrt{t_1};x_3=\sqrt{t_1};x_4=\sqrt{t_2};\)
\(x_1;x_2;x_3;x_4\) lập thành một cấp số cộng khi và chỉ khi :
\(x_2-x_1=x_3-x_2=x_4-x_3\)
\(\Leftrightarrow t_2=9t_1\left(a\right)\)
Áp dụng định lí Viet ta có : \(t_1+t_2=2\left(m+2\right);t_1.t_2=3+2m\left(b\right)\)
Từ (a) và (b) ta có : \(9m^2-14m-39=0\)
Đối chiếu điều kiện (*) ta có \(m=3\) hoặc \(m=-\frac{13}{9}\)
15 tháng 8 2021
Hàm số \(y=\left(m-2\right)x+m^2-3\) cắt đồ thị tại điểm có hoành độ bằng 4
\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)
\(\Leftrightarrow0=4\left(m-2\right)+m^2-3\)
\(\Leftrightarrow m^2+4m-11=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-2+\sqrt{15}\\m=-2-\sqrt{15}\end{matrix}\right.\)
CH
15 tháng 8 2021
Đồ thị cắt trục hoành tại điểm có hoành độ bằng 4 => A(4;0)
thay A(4;0) vào hàm số ta có:
\(\left(m-2\right).4+m^2-3=0\)
\(\Leftrightarrow4m-8+m^2-3=0\\ \Leftrightarrow m^2+4m-11=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2+\sqrt{15}\\m=-2-\sqrt{15}\end{matrix}\right.\)
NB
23 tháng 6 2021
1. hàm số nghịch biến khi
\(a< 0\\ \Leftrightarrow m-2< 0\\ \Leftrightarrow m< 2\)
2. \(y=\left(m-2\right)x+m+3\cap Ox,tại,x=3\)
\(\Rightarrow y=0\)
Có: \(0=\left(m-2\right)3+m+3\\ \Leftrightarrow0=4m-4\\ \Leftrightarrow m=\dfrac{3}{4}\)
3. pt hoành độ giao điểm của
\(y=-x+2,và,y=2x-1\) là
\(-x+2=2x-1\\ \Leftrightarrow3x=3\Leftrightarrow x=1\Rightarrow y=1\)
A(1,1)
3 đt đồng quy \(\Rightarrow A\in y=\left(m-2\right)x+m+3\\ \Rightarrow1=\left(m-2\right)1+m+3\\ \Leftrightarrow2m=0\\ \Leftrightarrow m=0\)
3 tháng 9 2021
Câu 2:
Thay x=0 và y=-3 vào (d), ta được:
m+2=-3
hay m=-5
22 tháng 8 2023
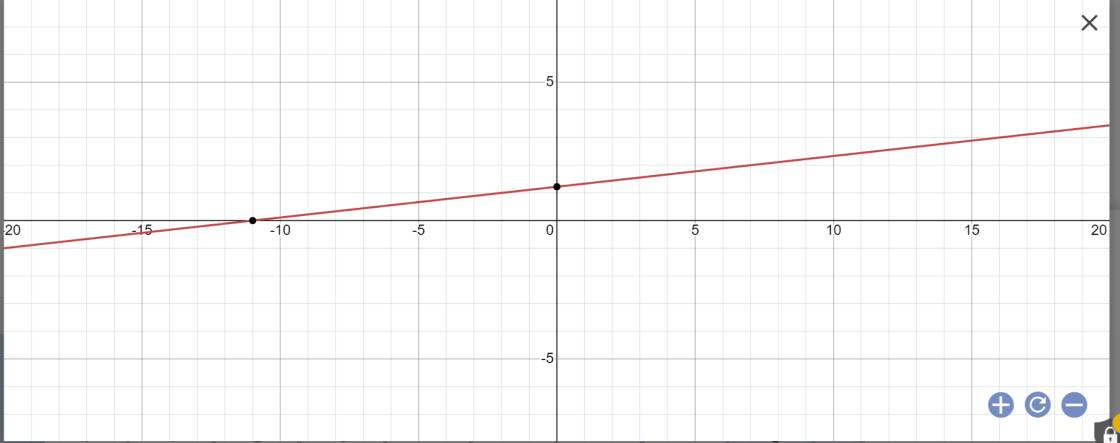
Thay x=-11 và y=0 vào (d), ta được:
-11(m-3)+2m-5=0
=>-11m+33+2m-5=0
=>-9m+28=0
=>m=28/9
=>(d): y=1/9x+56/9-5=1/9x+11/9
28 tháng 12 2020
- Xét phương trình hoành độ giao điểm :
\(x^2-3mx+m^2+1=mx+m^2\)
\(\Leftrightarrow x^2-4mx+1=0\) ( 1 )
Có : \(\Delta^,=4m^2-1\)
- Để (d) cắt ( P ) tại 2 điểm phân biệt trên trục hoành
<=> Phương trình ( 1 ) có 2 nghiệm phân biệt .
<=> \(\Delta^,=4m^2-1\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\le-\dfrac{1}{2}\\m\ge\dfrac{1}{2}\end{matrix}\right.\)
- Theo viets : \(\left\{{}\begin{matrix}x_1+x_2=4m\\x_1x_2=1\end{matrix}\right.\)
( đến đây giải nốt nhá hình như thiếu đề đoạn thỏa mãn :vvv )
Phương trình hoành độ giao điểm của đồ thị với trục hoành là :
\(x^3-2x^2+\left(1-m\right)x+m=0\left(1\right)\)
Biến đổi tương đương phương trình này :
\(\left(1\right)\Leftrightarrow x^3-2x^2+x-mx+m=0\)
\(\Leftrightarrow x\left(x^2-2x+1\right)-m\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-x-m\right)=0\Leftrightarrow x=1\) hoặc \(x^2-x-m=0\left(2\right)\)
Gọi \(x_1,x_2\) là nghiệm của phương trình (2) thì :
\(t^2+x_1^2+x_2^2< 4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2< 3\Leftrightarrow m< 1\) (*)
Yêu cầu bài toán tương đương với (2) có hai nghiệm phân biệt \(x_1;x_2\ne1\) thỏa mãn điều kiện (*)
\(\Leftrightarrow\begin{cases}\Delta=1+4m>0\\1^2-1-m\ne0\\m< 1\end{cases}\)\(\Leftrightarrow\begin{cases}-\frac{1}{4}< m< 1\\m\ne0\end{cases}\)