Cho hình bình hành ABCD có hai đỉnh A,B cố định, còn đỉnh C chạy trên một đường tròn (O;R). Tìm quỹ tích đỉnh D khi C thay đổi .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng phép tịnh tiến nha
Mà tìm quỹ tích C trong trường hợp nào hã bạn ???????????

Gọi I là trung điểm BC. Khi đó I G = 1 3 I A ⇒ G = V I ; 1 3
Mà A ∈ O ; R nên quỹ tích trọng tâm G của ∆ A B C là đường tròn O ; 1 3 R là ảnh của đường tròn ( O;R ), qua phép vị tự tâm I tỉ số k = 1 3
Đáp án A

Đáp án D
Gọi M, N lần lượt là trung điểm AB và CD.
Khi đó OM ⊥ AB và O’N ⊥ CD
Gọi I là giao điểm của MN và OO’
Đặt R = OA và h = OO’. Khi đó ΔIOM vuông cân tại O nên:
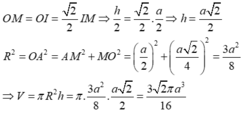

Đáp án A.
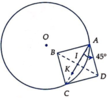
V A ; 2 2 A = K ⇒ K nằm giữa AC và AK = AD
Từ hình vẽ Q A ; 45 ° ( K ) = D
- Theo tính chất hình bình hành : BA=DC \(\Rightarrow\overrightarrow{AB}=\overrightarrow{CD}\). Nhưng theo giả thiết A,B cố định , cho nên \(\overrightarrow{AB}\) cố định . Ví C chạy trên (O;R) , D là ảnh của C qua phép tịnh tiến theo \(\overrightarrow{AB}\) , cho nên D chạy trên đường tròn O’ là ảnh của đường tròn O
- Cách xác định (O’) : Từ O kẻ đường thẳng // với AB , sau đó dựng véc tơ \(\overrightarrow{OO'}=\overrightarrow{AB}\). Từ O’ quay đường tròn bán kính R , đó chính là đường tròn quỹ tích của D.