Cho tam giác ABC. Tìm điểm m sao...
Đọc tiếp
Cho tam giác ABC. Tìm điểm m sao cho +
+2
=
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 2 2016
Bài 1: tam giác ABC, BM = 1/4BC, CB = 1/3AC. Nối MN, AM. Tìm tỉ số diện tích 2 tam giác ABM và MNC
Bài 2: cho tam giác ABC có DT là 100 xăng ti mét vuông. trên AB lấy điểm M sao cho AM = MB, trên BC lấy điểm N sao cho BN = NC và trên AC lấy điểm P sao cho AP = PC. nối M với N, N với P và P với M. tính DT tam giác MNP
bài 3: cho tam giác ABC, biết độ dày đáy BC là 27m, chiều cao AH là 20cm. trên AB lấy điểm M sao cho MA = MB. trên AC lấy điểm N sao cho NC = (1/3) AC. trên BC lấy điểm P sao cho BP = PC. Tính DT tam giác MNP
bài 4: cho tam giác ABC, M là điểm chính giữa BC, nối AM, trên AM lấy điểm N sao cho AN = 2 NM. DT tam giác ABN = 25 xăng ti mét vuông. Tính DT tam giác ABC
Thế này là quá nhiều bạn ạ
AH
Akai Haruma
Giáo viên
26 tháng 11 2021
Lời giải:
Kẻ chiều cao $CK, BH$. Ta có:
\(\frac{S_{MNC}}{S_{ANB}}=\frac{MN\times CK}{AN\times BH}=\frac{MN}{AN}\times \frac{CK\times MN}{BH\times MN}\)
\(=\frac{1}{2}\times \frac{S_{MNC}}{S_{BMN}}=\frac{1}{2}\times \frac{MC}{BM}=\frac{1}{2}\times \frac{3}{2}=\frac{3}{4}\)
1 tháng 1 2022
Trước hết ta cần chứng minh bổ đề sau (tạm gọi là bổ đề 1): Nếu 2 tam giác mà có chung đường cao tương ứng ( hay 2 đường cao tương ứng bằng nhau) thì tỉ số diện tích của hai tam giác bằng tỉ số cạnh đáy tương ứng.
Hạ đường cao chung AH của hai tam giác ABM và ACM. Ta cần chứng minh \(\frac{S_{ABM}}{S_{ACM}}=\frac{BM}{CM}\)
Thật vậy: \(S_{ABM}=\frac{1}{2}AH.BM\); \(S_{ACM}=\frac{1}{2}AH.CM\)
\(\Rightarrow\frac{S_{ABM}}{S_{ACM}}=\frac{\frac{1}{2}AH.BM}{\frac{1}{2}AH.CM}=\frac{BM}{CM}\)
Như vậy bổ đề được chứng minh.
1 tháng 1 2022
Một sự thật nghiệt ngã đó là muốn MN chia tam giác ABC thành 2 phần có diện tích bằng nhau thì chỉ còn nước M trùng với B mà thôi.
Muốn MN chia tam giác ABC thành 2 phần có dt bằng nhau thì điều hiển nhiên là \(\frac{S_{CMN}}{S_{ABC}}=\frac{1}{2}\)(dt tam giác CMN bằng một nửa dt tam giác ABC)
Giả sử M nằm trên cạnh BC nhưng M không trùng với B, ta sẽ có \(CM< BC\)\(\Leftrightarrow\frac{CM}{BC}< 1\)
Hai tam giác CMN và BCN có chung đường cao hạ từ N nên \(\frac{S_{CMN}}{S_{BCN}}=\frac{CM}{BC}\)(hai tam giác có chung đường cao thì tỉ số diện tích bằng tỉ số hai cạnh đáy tương ứng)
Từ đó ta có \(\frac{S_{CMN}}{S_{BCN}}< 1\)(1)
Mặt khác hai tam giác BCN và ABC có chung đường cao hạ từ B nên \(\frac{S_{BCN}}{S_{ABC}}=\frac{NC}{AC}\)
Do N nằm trên AC sao cho \(NA=NC\)nên \(\frac{NC}{AC}=\frac{1}{2}\)(NC bằng một nửa AC)
Từ đó \(\frac{S_{BCN}}{S_{ABC}}=\frac{1}{2}\)(2)
Nhân vế theo vế của (1) và (2), ta có: \(\frac{S_{CMN}}{S_{BCN}}.\frac{S_{BCN}}{S_{ABC}}< 1.\frac{1}{2}\)\(\Leftrightarrow\frac{S_{CMN}}{S_{ABC}}< \frac{1}{2}\)
Như vậy rõ ràng khi N không trùng với B thì việc MN chia tam giác ABC thành 2 phần có dt bằng nhau là không thể.
Do đó N trùng với B.
CM
22 tháng 11 2018
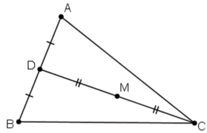
Gọi D là trung điểm AB.
Khi đó với mọi điểm M ta có :
⇔ M là trung điểm của trung tuyến từ đỉnh C.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 12 2022
38.
Gọi I là trung điểm AB và G là trọng tâm tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{MA}+\overrightarrow{MB}=2\overrightarrow{MI}\\\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\overrightarrow{0}\end{matrix}\right.\)
\(3\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=2\left|\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\right|\)
\(\Leftrightarrow3.\left|2\overrightarrow{MI}\right|=3\left|\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=2.\left|3\overrightarrow{MG}\right|\)
\(\Leftrightarrow6\left|\overrightarrow{MI}\right|=6\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow\left|\overrightarrow{MI}\right|=\left|\overrightarrow{MG}\right|\)
\(\Leftrightarrow MI=MG\)
\(\Rightarrow\) Tập hợp M là đường trung trực của đoạn thẳng IG
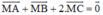
Gọi D là trung điểm của cạnh AB, ta có:
Đẳng thức đã cho trở thành:
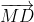2
+ 2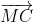
= 
=>
+
= 
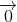
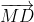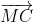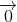
Đẳng thức này chứng tỏ M là trung điểm của CD