Trong kì thi THPT Quốc gia năm 2015, mỗi thí sinh có thể dự thi tối đa 8 môn : Toán, lí, hóa, sinh, văn , sử , địa và Tiếng Anh. Một trường Đại học dự kiến tuyển sinh dựa vào tổng điểm 3 môn trong kì thi chung và có ít nhất 1 trong hai môn là Toán hoặc Văn. Hỏi trường Đại học có bao nhiêu phương án tuyển sinh ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


só thí sinh dự môn toán là
120 x 20% = 24 thí sinh
số thí sinh sự thi môn tiếng anh là :
24 : 4/7 = 42 thí sinh
số thí sinh dự thi môn ngữ văn là
120 - ( 24 + 42 ) = 54 thí sinh
Số học sinh dự thi môn toán là :
120x20%=24(hs)
Số học sinh dự thi môn tiếng anh là:
24:4/7=42 (hs)
Số học sinh dự thi môn văn là:
120-24-42=54(hs)
ĐS :

Đáp án C.
Phương pháp:
Xác suất của biến cố A:
P A = n A n Ω .
Cách giải:
Số phần tử của không gian mẫu : n Ω = 24 4
A: “Bình và Lan có chung đúng một mã đề thi”
- Chọn một môn chung mã đề thi có : 2 cách
- Chọn một mã chung có: 24 cách
- Chọn mã môn còn lại:
+) Cho Bình: 24 cách
+) Cho Lan: 23 cách
Xác suất:
P A = n A n Ω = 2.24.24.23 24 4 = 23 288

Số học sinh thi môn toán là :
20% . 120 = 24 ( học sinh )
Số học sinh thi môn Anh là :
24 : \(\frac{4}{7}\)= 42 ( học sinh )
Số học sinh thi môn văn là :
120 - 24 - 42 = 54 ( học sinh )
Số học sinh dự thi Van chiếm số % tổng số thí sinh là :
\(\frac{54.100}{120}\%=\)45%
Đáp số : 45% .
Học tốt

Chọn B
Số phần tử của không gian mẫu là ![]()
- Gọi A là biến cố “3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”
- Số phần tử của biến cố A là
![]()
Vậy xác suất để xảy ra biến cố A là
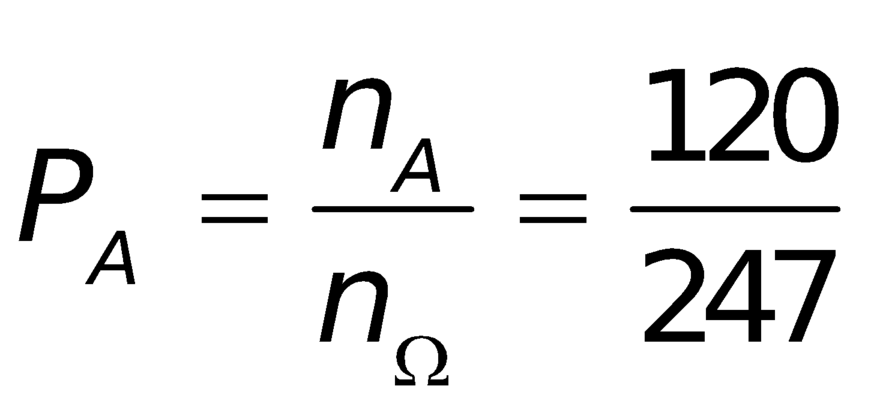 .
.

a) Số học sinh dự thi môn ngữ văn là:
120 . 20% = 24 ( học sinh )
Số học sinh dự thi môn tiếng anh là:
24 . 4/7 = 42 ( học sinh )
b) Số học sinh dự thi môn toán là:
120 - ( 24 + 42 ) = 54 ( học sinh )
Tỉ số phần trăm số học sinh dự thi môn toán và tổng số học sinh dự thi là:
54 . 100 : 120 = 45 ( % )

Chọn C.
Hai bạn Bình và Lan cùng 1 mã đề, cùng 1 môn thi (Toán hoặc TA) có 24 cách.
Môn còn lại khác nhau ⇒ có 24.23 cách chọn.
Do đó, có 2.24.24.23 = 26496 cách để Bình, Lan có chung mã đề.
Vậy xác suất cần tính là P = 26496 24 2 . 24 2 = 23 288 .

Nếu bớt 1/4 số hs dự thi môn toán, 1/7 số hs dự thi môn anh, thêm vào 1/5 số học sinh dự thi môn văn thì số hs dự thi 3 môn bằng nhau
=> 3/4 số hs dự thi môn toán=6/7 số hs dự thi môn anh=6/5 số hs dự thi môn văn
Quy ước số hs dự thi môn Anh là 1 đơn vị
P/s chỉ số hs dự thi môn toán so với số học sinh dự thi môn anh là: 6/7:3/4=8/7( số hs dự thi môn anh)
P/s chỉ số hs dự thi môn văn so với số hs dự thi môn anh là: 6/7:6/5=5/7( số hs dự thi môn anh)
P/s chỉ 200 hs so với số hs dự thi môn anh là: 1+8/7+5/7= 20/7
Số hs dự thi môn anh là: 200:20/7= 70(hs)
Số hs dự thi môn toán là: 70.8/7= 80(hs)
Số hs dự thi môn văn là 70.5/7= 50(hs)



Trường hợp 1 : Trường đại học chỉ xét 1 trong 2 môn Toán hoặc Văn :
Có : \(2.C_6^2=30\) cách
Trường hớp 2 : Trường đại học xét cả 2 môn Toán và Văn :
Có : \(1.C_6^2=6\) cách
Vậy có các trường hợp là : 30+6=36 cách
fggfdfg