Question

[Hậu Duệ Mặt Trời]

Cho phản ứng hạt nhân sau: \(\alpha + _7^{14}N \rightarrow p + _8^{17} O\) . Hạt α chuyển động với động năng 9,7 MeV đến bắn vào hạt N đứng yên, sau phản ứng hạt p có động năng 7,0 MeV. Cho biết: m_N = 14,003074 u; m_p = 1,007825 u; m_O = 16,999133 u; mα = 4,002603 u. Xác định góc giữa các phương chuyển động của hạt α và hạt p ?

A.25^o.

B.41^o.

C.52^o.

D.60^o.

Answer 1

[Hoc247]

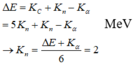
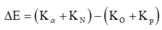
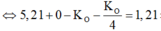
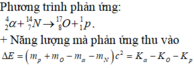
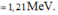
\(\alpha + _7^{14}N \rightarrow p + _8^{17} O\)

 \(m_t-m_s = m_{\alpha}+m_N - (m_p+m_O) = -1,281.10^{-3}u < 0\), phản ứng là thu năng lượng.

Sử dụng công thức: \(W_{thu} = (m_s-m_t)c^2 = K_t-K_s\)

=> \(1,285.10^{-3}.931 = K_{\alpha}+K_N-( K_p+K_O)\) (do N đứng yên nên K_N = 0)

=> \(K_{O} = 1,5074MeV.\)

Áp dụng định luật bảo toàn động lượng

\(\overrightarrow P_{\alpha} =\overrightarrow P_{p} + \overrightarrow P_O \)

Dựa vào hình vẽ ta có 

Áp dụng định lí hàm cos trong tam giác

\(P_{\alpha}^2+ P_{p}^2 -2 P_{\alpha}P_{p}\cos{\alpha} = P_{O}^2\)

=> \(\cos {\alpha} = \frac{P_{\alpha}^2+P_p^2-P_O^2}{2P_{\alpha}.P_{p}} = \frac{2m_{\alpha}K_{\alpha}+2m_pK_P-2.m_O.K_O}{2.\sqrt{2.m_{\alpha}K_{\alpha}.2.m_p.K_p}} \)

=> \(\alpha \approx 52^016'\).

 

Answer 2

[Học Mãi]

Cảm ơn lời giải của bạn Hoc247 nhé.