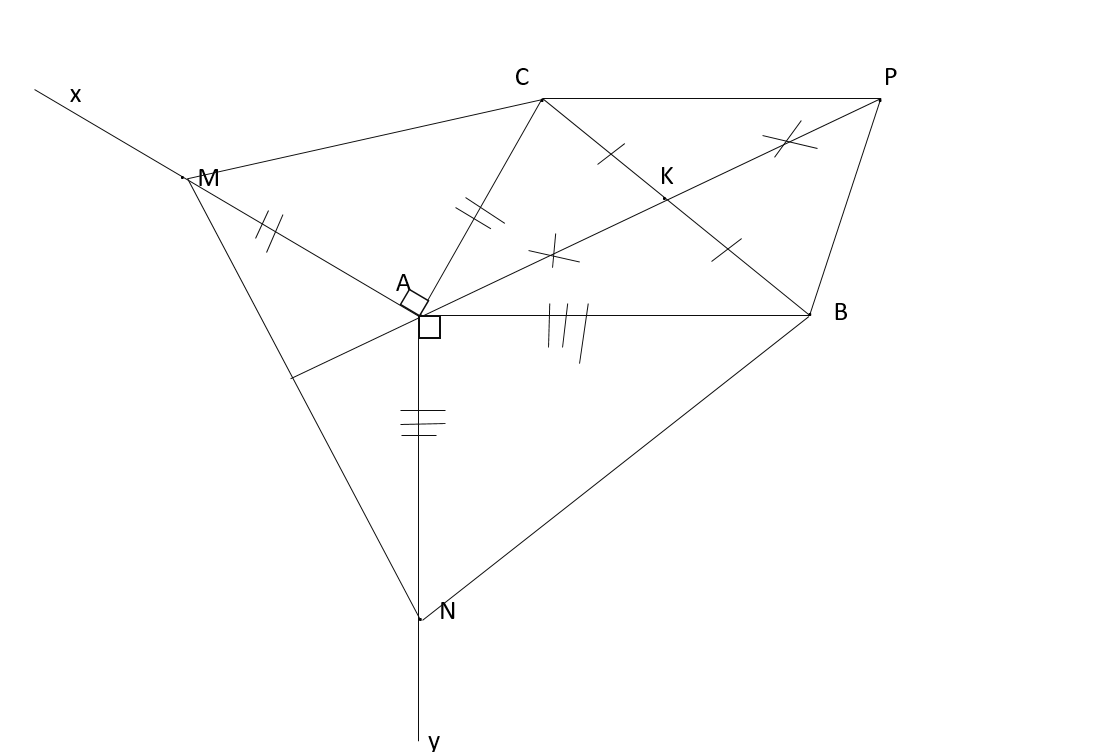
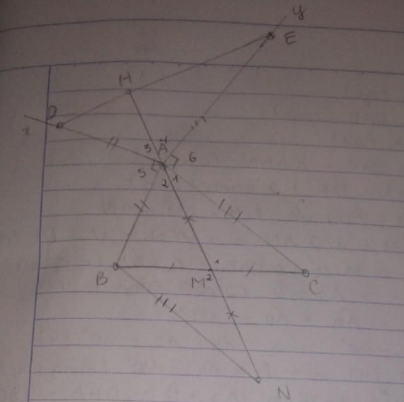
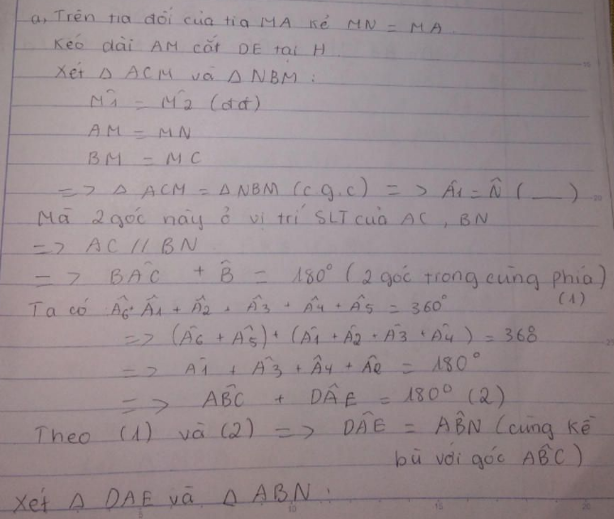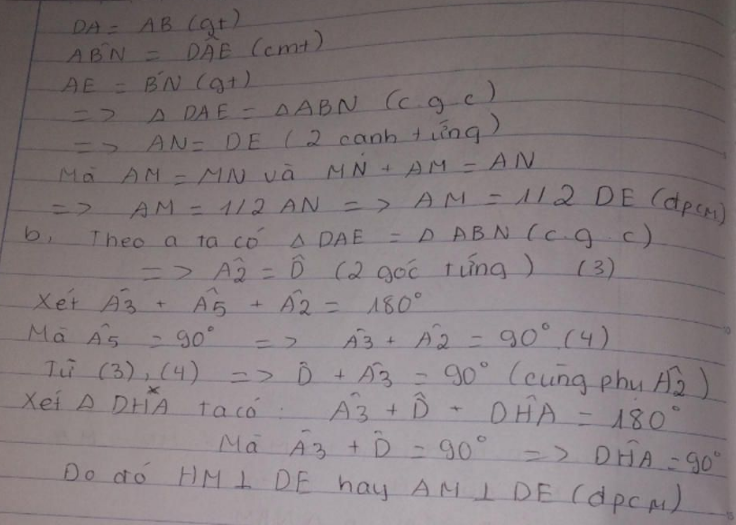Cho tam giác ABC có A < 90 độ. Gọi M là trung điểm cạnh BC. Trên nửa mặt phẳng bờ AB không chứa điểm C kẻ tia Ax vuông góc với AB, trên tia Ax lấy điểm D sao cho AD=AB. Trên nửa mặt phẳng bờ AC không chứa điểm B kẻ Ay vuông góc với AC. Trên tia Ay lấy điểm E sao cho AE=AC. Trên tia đối MA lấy MN=MA. Chứng minh:
a) BN=AE b) AM=\(\frac{DE}{2}\)
c) AM vuông góc với DE
;-;