cho mik hỏi
1 ô tô chuyển động trên quãng đường 270 với vận tốc 45km/h . Biết nữa thời gian đầu đi với vận tốc 50 km/h
a. Tính thời gian ô tô đi được
b. Tính chiều dài quãng đường đầu
c. Tính vận tốc trong nữa thời gian sau
giúp mik zs tấu ney mik phải nộp rồi


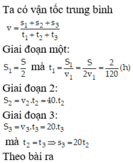
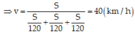

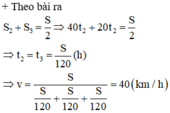
a) thời gian ô tô đi được là:
t=\(\frac{s}{v}=\frac{270}{45}=6\left(h\right)\)
b) chiều dài quãng đường đầu là
s=v'.\(\frac{t}{2}\)=50.\(\frac{6}{2}\)=150(km)
chiều dài quãng đường còn lại cần đi là:
s''=s-s'=270-150=120(km)
Vận tốc phái đi là:
v=\(\frac{s''}{\frac{t}{2}}=\frac{120}{\frac{6}{2}}=40\)(km/h)