Một vật có khối lượng m=200g chuyển động dọc theo trục Ox dưới tác dụng của lực tổng hợp là F=2-80x với x là toạ độ của vật đo được băng m, F đo bằng N với biên độ A=7,5cm . Trong quá trình dao động vật có vận tốc cực đại bằng :
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1 tháng 8 2017
Chọn C.
Đối chiếu F = - 0 , 96 cos 4 t với biểu thức tổng quát
F = - m ω 2 A cos ( ω t + φ )
VT
22 tháng 5 2019
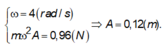
+ Đối chiếu F = − 0 , 96 cos ( 4 t + π / 4 ) ( N ) với biểu thức tổng quát F = - m ω 2 A cos ( ω t + φ ) :
ω = 4 ( r a d / s ) m ω 2 A = 0 , 96 N ⇒ A = 0 , 12 m
Chọn đáp án C
VT
25 tháng 10 2017
Đáp án D
Độ giãn của con lắc ở vị trí cân bằng:
T = 0 , 4 s = 2 π Δ l 0 g ⇒ Δ l 0 = T 2 . g 4 π 2 = 0 , 04 m = 4 cm
Lực đàn hồi của con lắc tại hai vị trí biên:
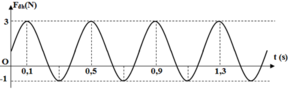
F dhmax = k Δ l 0 + A = 3 F dhmin = k Δ l 0 − A = − 1 ⇒ Δ l 0 + A Δ l 0 − A = − 3 1 ⇒ A = 2 Δ l 0 = 8 cm
Độ cứng của lò xo: k = F dhmax Δ l 0 + A = 3 0 , 04 + 0 , 08 = 25 N / m
Biểu thức lực đàn hồi:
F dh = k Δ l 0 + x = kΔ l 0 + k . x = 1 + 2 cos 5 πt + φ
Tại thời điểm t=0,1s, lực đàn hồi có giá trị F=3N nên: F dh = 1 + 2 cos 5 π . 0 , 1 + φ = 3
⇒ cos 0 , 5 π + φ = 1 ⇒ 0 , 5 π + φ = 0 ⇒ φ = − 0 , 5 π = − π 2
Phương trình dao động của vật: x = 8 cos 5 πt − π 2 cm
VT
25 tháng 7 2018
Chọn A
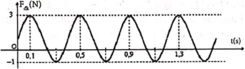
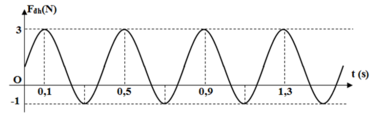
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
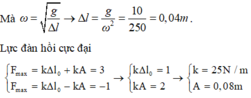
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại → φ 0 = π 2 rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm.
VT
18 tháng 11 2018
Đáp án D
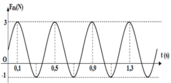
Từ đồ thị ta thấy T = 0,4 s → ω = 5π rad/s.
Mà
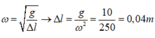
Lực đàn hồi cực đại
Từ t = 0 đến t = 0,1 s (trong khoảng thời gian T/4) lực đàn hồi tăng đến giá trị cực đại
→ 
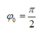rad.
→ Phương trình li độ x = 8cos(5πt + π/2) cm
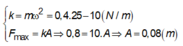
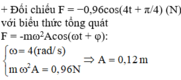
Đặt F' = F-2, suy ra: F'=-80.x là lực hồi phục (F=-k.x)
Vậy k = 80(N/m)
\(\Rightarrow \omega = \sqrt{\dfrac{k}{m}}= \sqrt{\dfrac{80}{0,2}}=4\pi(rad/s)\)
Tốc độ cực đại: \(v_{max}=\omega A = 4\pi.7,5=30\pi (cm/s)\)
vậy là đáp án nào bạn