Cho hình hộp ABCD.A'B'C'D'. Gọi M. N theo thứ tự là trọng tâm của cá tam giác BDA', B'D'C'. Chứng minh rằng A,C',M,N thẳng hàng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
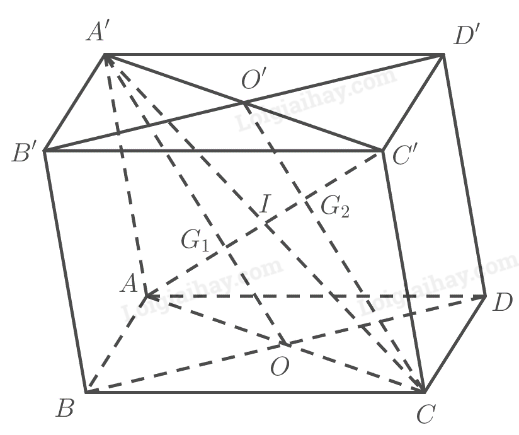
Gọi \(O = AC \cap B{\rm{D}},O' = A'C' \cap B'{\rm{D}}',I = AC' \cap A'C\)
Vì \(AA'\parallel CC',AA' = CC'\) theo tính chất hình hộp nên \(AA'C'C\) là hình bình hành \( \Rightarrow I\) là trung điểm của \(AC'\) và \(A'C\).
Ta có: \({G_1}\) là trọng tâm của tam giác \(BDA' \Rightarrow \frac{{A'{G_1}}}{{A'O}} = \frac{2}{3}\)
Tam giác \(AA'C\) có \(\frac{{A'{G_1}}}{{A'O}} = \frac{2}{3}\) nên \({G_1}\) là trọng tâm của tam giác \(AA'C\)
Mà \(I\) là trung điểm của \(A'C\) nên \(\frac{{A{G_1}}}{{AI}} = \frac{2}{3} \Rightarrow A{G_1} = \frac{2}{3}AI\)
Mà \(AI = \frac{1}{2}AC'\)
\( \Rightarrow A{G_1} = \frac{1}{3}AC'\left( 1 \right)\)
Ta có: \({G_2}\) là trọng tâm của tam giác \(B'D'C \Rightarrow \frac{{C{G_2}}}{{CO'}} = \frac{2}{3}\)
Tam giác \(ACC'\) có \(\frac{{C{G_2}}}{{CO'}} = \frac{2}{3}\) nên \({G_2}\) là trọng tâm của tam giác \(ACC'\)
Mà \(I\) là trung điểm của \(AC'\) nên \(\frac{{C'{G_2}}}{{C'I}} = \frac{2}{3} \Rightarrow C'{G_2} = \frac{2}{3}C'I\)
Mà \(C'I = \frac{1}{2}AC'\)
\( \Rightarrow C'{G_2} = \frac{1}{3}AC'\left( 2 \right)\)
Từ (1) và (2) suy ra \({G_1}\) và \({G_2}\) chia đoạn \(AC\) thành ba phần bằng nhau.
QD
31 tháng 3 2017
Lời giải:
a) Tứ giác DBB'D' là hình bình hành nên BD // B'D' . Vì vậy BD // (B'D'C) và BA' // CD' \(\Rightarrow\) BA' // ( B'D'C).
Từ đó suy ra ( BDA') //B'D'C).
b) Gọi ,
là giao điểm của AC' với A'O và CO'.
Do \(G_1=A'O\cap AI\) và A'O và AI là hai đường trung tuyến của tam giác nên \(G_1\) là trọng tâm của tam giác A'AC.
Chứng minh tương tự \(G_2\) là trọng tâm tam giác CAC'.
Suy ra \(\dfrac{AG_1}{AO}=\dfrac{2}{3}\); \(\dfrac{CG_2}{CO}=\dfrac{2}{3}\) nên đường chéo AC' đi qua trọng tâm của hai tam giác BDA' và B'D'C.
c) Do O và O' lần lượt là trung điểm của AC và A'C' nên \(OC=A'O'\) và OC' // A'O'.
Vì vậy tứ giác OCO'A là hình bình hành và OA'//OC.
Từ đó ta chứng minh được \(G_1\) lần lượt là trung điểm của \(AG_1\) và \(G_2\) là trung điểm của \(G_1C'\).
Do đó: \(AG_1=G_1G_2=G_2C\) (đpcm).
d) \(\left(A'IO\right)=\left(AA'C'C\right)\). Nên thiết diện cần tìm là (AA'C'C).
3 tháng 12 2021
a: Xét tứ giác BPNC có
G là trung điểm của BN
G là trung điểm của PC
Do đó: BPNC là hình bình hành
Đặt \(\overrightarrow{AA'}=\overrightarrow{a}\), \(\overrightarrow{AB'}=\overrightarrow{b}\) và \(\overrightarrow{AD}=\overrightarrow{d}\)
Theo quy tắc hình bình hành ta có :
\(\overrightarrow{AC'}=\overrightarrow{AA'}+\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{d}\)
Mà \(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{d}=\overrightarrow{AA'}+\overrightarrow{AB}+\overrightarrow{AD}=3\overrightarrow{AM}\)
Suy ra \(\overrightarrow{AC'}=3\overrightarrow{AM}\)
Do đó A, M, C' thẳng hàng
Tương tự cũng có C', N, A thẳng hàng. Suy ra điều cần chứng minh