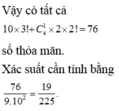Lấy một số trong tập hợp tất cả các số tự nhiên có 9 chữ số khác nhau.Tính xác suất để số lấy ra là số chia hết cho9 ??
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
25 tháng 8 2018
Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: 
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: 
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: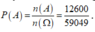 
CM
11 tháng 1 2019
Chọn A
Giả sử số cần lập là 
Số phần từ không gian mẫu: 
Gọi A là biến cố lấy được số chia hết cho 11 và tổng của các chữ số của chúng cũng chia hết cho 11.
Ta có:
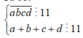
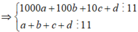
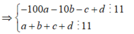
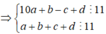
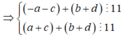
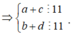
Từ 1,2,3,4,5,6,7,8,9 ta có 4 cặp tổng chia hết cho 11 là: 
CM
21 tháng 5 2018
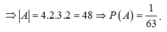
Chọn A
+) Không gian mẫu Ω = “Chọn ngẫu nhiên một số trong các số tự nhiên có 3 chữ số”.=> | Ω | = 9. 10 2
+) Biến cố A = “Số tự nhiên được chọn chia hết cho 9 và các chữ số đôi một khác nhau”.
Ta tìm số các số tự nhiên gồm 3 chữ số khác nhau và chia hết cho 9 (tổng các chữ số là một số chia hết cho 9).
Bộ ba số (a;b;c) với a,b,c ∈ [0;9](a,b,c đôi một khác nhau ) và a + b + c = 9m, m ∈ ℕ * được liệt kê dưới đây:
Vậy có tất cả 10.3! + 4.2.2! = 76 => | Ω A | = 76
Xác suất cần tính bằng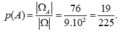 
CM
9 tháng 1 2018
Chọn A
Ta có tất cả các số tự nhiên có 7 chữ số bắt đầu từ 1000000 đến 9999999 gồm 9000000 số.
Do đó 
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 3.
Mà 
nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
128571 bộ 70 số tự nhiên liên tiếp có 128571 số thỏa mãn yêu cầu
30 số cuối có 3 số tận cùng bằng 3 được xét trong bảng sau
| 9999973 |
9999983 |
9999993 |
| Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 4 |
Vậy tất cả có 128572 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3.
Gọi A là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3’ thì n(A) = 128572
Suy ra 
CM
8 tháng 11 2019
Chọn A
Ta có tất cả các số tự nhiên có 7 chữ số bắt đầu từ 1000000 đến 9999999 gồm 9000000 số.
Do đó 
Mặt khác, ta thấy cứ 70 số tự nhiên liên tiếp thì có 10 số chia hết cho 7, trong đó có 1 số có chữ số hàng đơn vị là chữ số 3.
Mà 90000 = 70x128571 + 30, nên ta chia 9000000 số thành 128571 bộ 70 số liên tiếp và còn lại 30 số cuối, trong đó:
128571 bộ 70 số tự nhiên liên tiếp có 128571 số thỏa mãn yêu cầu
30 số cuối có 3 số tận cùng bằng 3 được xét trong bảng sau
| 9999973 |
9999983 |
9999993 |
| Chia cho 7 dư 4 |
Chia hết cho 7 |
Chia cho 7 dư 4 |
Vậy tất cả có 128572 số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3.
Gọi là biến cố ‘Chọn được một số chia hết cho 7 và chữ số hàng đơn vị là chữ số 3’ thì n(A) = 128572
Suy ra 