cho tam giác ABC vuông tại A và B = 30o .Tính các giá trị của biểu thức sau:a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)B) ...
Đọc tiếp
cho tam giác ABC vuông tại A và B = 30o .Tính các giá trị của biểu thức sau:
a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)
B) \(\sin\left(\overrightarrow{AB},\overrightarrow{AC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{BA}\right)+\cos\overrightarrow{CA},\overrightarrow{BA}\)
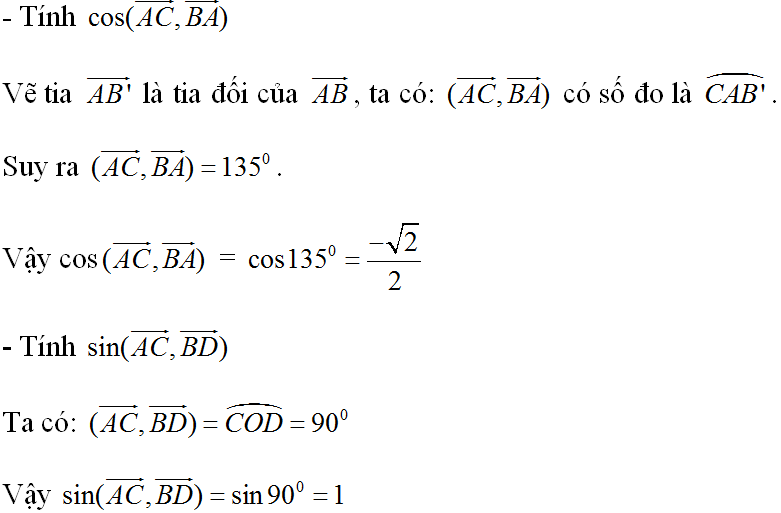
Do tam giác ABC vuông tại A và \(\widehat{B}=30^o\) \(\Rightarrow C=60^o\)
\(\Rightarrow\left(\overrightarrow{AB},\overrightarrow{BC}\right)=150^o;\)\(\left(\overrightarrow{BA},\overrightarrow{BC}\right)=30^o;\left(\overrightarrow{AC},\overrightarrow{CB}\right)=120^o\)
\(\left(\overrightarrow{AB},\overrightarrow{AC}\right)=90^o;\left(\overrightarrow{BC},\overrightarrow{BA}\right)=30^o\).Do vậy:
a) \(\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\sin\left(\overrightarrow{BA},\overrightarrow{BC}\right)+\tan\frac{\left(\overrightarrow{AC},\overrightarrow{CB}\right)}{2}\)
\(=\cos150^o+\sin30^o+\tan60^o\)
\(=-\frac{\sqrt{3}}{2}+\frac{1}{2}+\sqrt{3}\)
\(=\frac{\sqrt{3}+1}{2}\)
b) \(\sin\left(\overrightarrow{AB},\overrightarrow{AC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{AB}\right)+\cos\left(\overrightarrow{CA},\overrightarrow{BA}\right)\)
\(=\sin90^o+\cos30^o+\cos0^o\)
\(=1+\frac{\sqrt{3}}{2}\)
\(=\frac{2+\sqrt{3}}{2}\)