1 người gánh 1 bao gạo 100 niutơn và 1 thùng mì nặng 200 niutơn. Đòn gánh dài 1,2 mét. Khi đòn gánh thăng bằng vai người đó phải đạt tại điểm nào ? Bỏ qua khối lượng của đòn gánh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
24 tháng 8 2019
Hình biểu diễn lực:
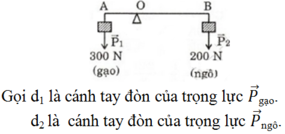
Áp dụng quy tắc hợp lực hai lực song song cùng chiều:
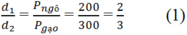
Mặt khác ta có:
d1 + d2 = AB = 1 m (2)
Từ (1), (2) ta có hệ phương trình sau: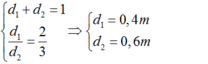
Vai người gánh chịu một lực là:
P = Pgạo + Pngô = 300 + 200 = 500 (N).
DQ
30 tháng 1 2021
Gọi trọng lượng của thùng gạo và thùng ngô lần lượt là \(P_1\) và \(P_2\).
Khoảng cách từ thùng gạo và thùng ngô đến điểm đặt của đòn gánh trên vai là \(d_1\) và \(d_2\).
Ta có:
\(P_1d_1=P_2d_2\)
\(\Rightarrow300d_1=200d_2\)
\(\Rightarrow d_2=1,5d_1\)
Mà \(d_1+d_2=1,5\) (m)
\(\Rightarrow d_1=0,6\) (m) và \(d_2=0,9\) (m)
Vậy vai người đó đặt điểm cách vị trí trí treo thùng gạo trên đòn gánh là 0,6 m và chịu lực: \(F=P_1+P_2=500\) (N)
16 tháng 12 2015
Áp dụng quy tắc hợp lực song song cùng chiều, ta được:
\(\frac{F_1}{F_2}=\frac{d_2}{d_1}\Rightarrow\frac{d_2}{d_1}=\frac{300}{200}=\frac{3}{2}\)
Mà \(d_1+d_2=1\)
\(\Rightarrow\begin{cases}d_1=0,4m\\d_2=0,6m\end{cases}\)
Lực mà vai người phải chịu: \(F=F_1+F_2=300+200=500N\)
Y
17 tháng 5 2023
\(F_1=300N;F_2=200N\)
\(d=1m\)
\(d_1=?\) \(d_2=?\)
\(F=?\)
==================================
Ta có :
\(\left\{{}\begin{matrix}F=F_1+F_2\\\dfrac{F_1}{F_2}=\dfrac{d_2}{d_1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}F=300+200=500\left(N\right)\\\dfrac{300}{200}=\dfrac{d_2}{d_1}\Rightarrow\dfrac{3}{2}=\dfrac{d_2}{d_1}\left(1\right)\end{matrix}\right.\)
Lại có : \(d=d_1+d_2\Rightarrow d_1+d_2=1\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}3d_1-2d_2=0\\d_1+d_2=1\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}d_1=0,4\left(m\right)\\d_2=0,6 \left(m\right)\end{matrix}\right.\)
Vậy người đó phải đặt đòn gánh cách vai là \(0,4m\) và \(0,6m\) . Phải chịu 1 lực bằng \(500N\).
16 tháng 4 2017
Gọi O là điểm đặt của vai.
Áp dụng quy tắc hợp lực song song cùng chiều ta có:
Ta có: P= P1 + P2 = 300+ 200 = 500N
P1. OA = P2. OB => =
=
=
=> =
(1)
Mặt khác: AB = OA +OB (2)
(1) & (2) => OA = 40cm và OB = 60cm
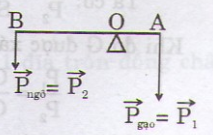
Gọi trọng lượng của bao gạo là P1 ; trọng lượng của thùng mì là P2 ; khoảng cách từ điểm tựa -> điểm đặt bao gạo là OO1 ; khoảng cách từ điểm
tựa -> điểm đặt thùng mì là OO2 .
Theo nguyên lí cân = của đòn bẩy , ta có : \(\frac{OO_1}{OO_2}=\frac{P_2}{P_1}=\frac{200}{100}=2\)=> Vai người đó phải đặt ở điểm sao cho OO1 = 2OO2
Giả sử vị trí đặt vai cách bao gạo là d, cách thùng mì là d'
\(\Rightarrow d+d'=1,2\)(1)
Khi đòn gánh thăng bằng ta có: \(\dfrac{d}{d'}=\dfrac{200}{100}=2\) (2)
Rút d' ở (2) thế vào (1) ta tìm được: d = 0,8m và d'=0,4m