1.Trên màn, trong khoảng giữa hai vân sáng liên tiếp có màu giống màu của vân trung tâm còn có chín vân sáng khác.
2.Trên một miền nào đó người ta thấy tổng cộng 21 vân sáng trong đó có 3 vân sáng trùng nhau và 2 trong 3 vân trùng nằm ở 2 đầu của miền này
cac thấy cho em hỏi trong công thức : k1λ1=k2λ2 thì K1 với K2 là só bậc hay là số vân và trong trong câu 1 và câu 2 thì công thức k1λ1=k2λ2 được áp dung như thế nào ? mong thay cô giúp e cái này khó hiểu quá



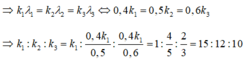
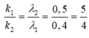
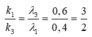
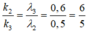
@Đào Hiếu Ở công thức câu 2 phải trừ đi 1 là do trừ đi vân trùng ở chính giữa em nhé.
Công thức muốn lập ra được thì ta cần phải hiểu bản chất của nó tại sao lại suy được như vậy.
Câu 1: Giữa 2 vân sáng liên tiếp: \(x_{Trùng}=k_1i_1=k_2i_2\) (*), để đơn giản ta xét từ vân trung tâm thì \(k_1 , k_2\) là bậc vân sáng. Không kế vân trung tâm, thì số vân sáng quan sát được trên đoạn trùng nhau là: \(k_1+k_2-1\)(vì có 1 vị trí trùng nên ta trừ đi 1).
Nếu tìm số vân sáng trong khoảng giữa hai vân liên tiếp thì là: \(k_1+k_2-2\) (do không tính vân trùng)
\(\Rightarrow k_1+k_2-2=9\Rightarrow k_1 + k_2=11\), rút k1 thay vào (*) thì ta đc phương trình như của bạn.
Câu 2: Tương tự, \(x_{Trùng}=k_1i_1=k_2i_2\)(**) - Tính từ vân trung tâm đi lên bạn nhé
Vì đề bài nói là trên miền nào đó, nên ta tính cả hai đầu
\(\Rightarrow k_1+k_2-2+1=21\)(Trừ 2 vị trí trùng nhau cộng với vân trung tâm, mỗi vị trí trùng ta chỉ tính 1 lần)
\(\Rightarrow k_1 + k_2=22\)
Rút k1 thế vào (**) ta được pt tương tự như bạn.
Giả sử M là điểm gần nhất cùng màu với vân trung tâm O, suy ra M là vị trí trùng nhau của vân 1 và 2.
Mà tại M là vị trí vân sáng của 1 và 2 nên \(MO = k_1i_1=k_2i_2\)(với \(k_1:k_2\) tối giản, do 2 vân gần nhau nhất)
\(\Rightarrow k_1\dfrac{\lambda_1 D}{a}=k_2\dfrac{\lambda_2 D}{a}\Rightarrow k_1\lambda_1=k_2\lambda_2\)