Chọn câu đúng.
Hai nguồn kết hợp là hai nguồn có
A.cùng biên độ.
B.cùng tần số.
C.cùng pha ban đầu.
D.cùng tần số, hiệu số pha không đổi theo thời gian.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
28 tháng 1 2018
Đáp án B
Phương pháp: Phương trình giao thoa sóng trong giao thoa sóng hai nguồn cùng pha:
u M = 2 acos π ( d 2 - d 1 ) λ cos [ ωt - π ( d 2 + d 1 ) λ ]
Cách giải:
Bước sóng: λ = 2cm
Phương trình sóng tại M:
u M = 2 acos π ( MA - MB ) λ cos [ ωt - π ( MA + MB ) λ ]
X là điểm dao động với biên độ cực đại và ngược pha với M.
Phương trình sóng tại X:
u X = 2 acos π ( XA - XB ) λ cos [ ωt - π ( XA + XB ) λ ]
Vì X và M thuộc elip => M + MB = X + XB
=> uM và uX chỉ khác nhau về:
cos π ( MA - MB ) λ ; cos π ( XA - XB ) λ
Vì M thuộc trung trực của AB
⇒ cos π ( MA - MB ) λ = 1
X ngược pha với M
⇔ cos π ( XA - XB ) λ = - 1 ⇔ X A - X B = ( 2 k + 1 ) λ
- AB ≤ ( 2 k + 1 ) λ ≤ AB ⇔ - 19 ≤ ( 2 k + 1 ) λ ≤ 19 ⇒ - 5 , 25 ≤ k ≤ 4 , 25
=> Có 10 điểm dao động với biên độ cực đại và ngược pha với M trên đoạn B
=> Trên elip có 20 điểm dao động với biên độ cực đại và ngược pha với M.
VT
11 tháng 3 2018
Đáp án B
Phương pháp: Phương trình giao thoa sóng trong giao thoa sóng hai nguồn cùng pha:
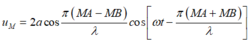
X là điểm dao động với biên độ cực đại và ngược pha với M.
Phương trình sóng tại X:
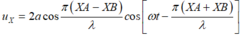
Vì X và M thuộc elip => M + MB = X + XB
=> Có 10 điểm dao động với biên độ cực đại và ngược pha với M trên đoạn B
=> Trên elip có 20 điểm dao động với biên độ cực đại và ngược pha với M
VT
7 tháng 10 2019
Chọn D
+Biên độ sóng tại M:
A M = 2 a cos π d 1 - d 2 λ = 2 a cos π d 1 - d 2 v f =0 cm
HY
23 tháng 9 2015
Giữa M và đường trung trực của AB có hai đường cực đại khác tức là M nằm ở đường cực đại thứ k = 3. (Vì đường trung trực của AB với AB cùng pha là cực đại với k = 0)
=> \(AM - BM = 3 \lambda\)
=> \(20 - 15.5 = 3 \lambda \)
=>\(3 \frac{v}{f} = 4,5cm\)
=>\(f = \frac{3v}{4,5} = 20Hz.\)
Chọn đáp án. A
4 tháng 5 2016
Ta có \(\lambda=\frac{v}{f}=\frac{200}{10}=20\left(cm\right)\). Do M là một cực đại giao thoa nên để đoạn AM có giá trị lớn nhất thì M phải nằm trên vân cực đại bậc 1 như hình vẽ ở dưới và thõa mãn:
\(d_2-d_1=k\lambda=1.20=20\left(cm\right)\) (1). ( do lấy k= +1)
Mặt khác, do tam giác AMB là tam giác vuông tại A nên ta có :
\(BM=d_2=\sqrt{\left(AB\right)^2+\left(AM\right)^2}=\sqrt{40^2+d^2_1}\) (2). Thay (2) vào (1)
ta được : \(\sqrt{40^2+d^2_1}-d_1=20\Rightarrow d_1=30\left(cm\right)\)
\(\rightarrow\) Đáp án B
VT
1 tháng 1 2019
Đáp án C
+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:
- A B λ < k < A B λ ⇔ - 10 1 , 5 < k < 10 1 , 5 ⇔ - 6 , 67 < k < 6 , 67 ⇒ k = 0 ; ± 1 , ± 2 , . . . . , ± 6
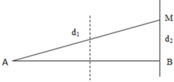
+ Ta có: S A M B = 1 2 A B . M B ⇒ ( S A M B ) m i n ⇔ ( M B ) m i n ⇔ M thuộc cực đại ứng với kmax => d1 – d2 = 6λ = 9cm.
+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
A B 2 + d 2 2 = d 1 2 ⇔ 10 2 + d 2 2 = ( d 2 + 9 ) 2 ⇒ d 2 = 19 18 c m = M B ⇒ S A M B = 1 2 A B . M B = 1 2 . 10 . 19 18 = 5 , 28 c m 2
VT
13 tháng 7 2017
Đáp án C
+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:
+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
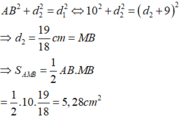
Hai nguồn kết hợp là hai nguồn có cùng tần số, hiệu số pha không đổi theo thời gian.