chứng minh rằng nếu a+b=1 thì a^2+b^2>=1/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TG
Trúc Giang
24 tháng 7 2021
Đúng(0)
Những câu hỏi liên quan
3 tháng 5 2017
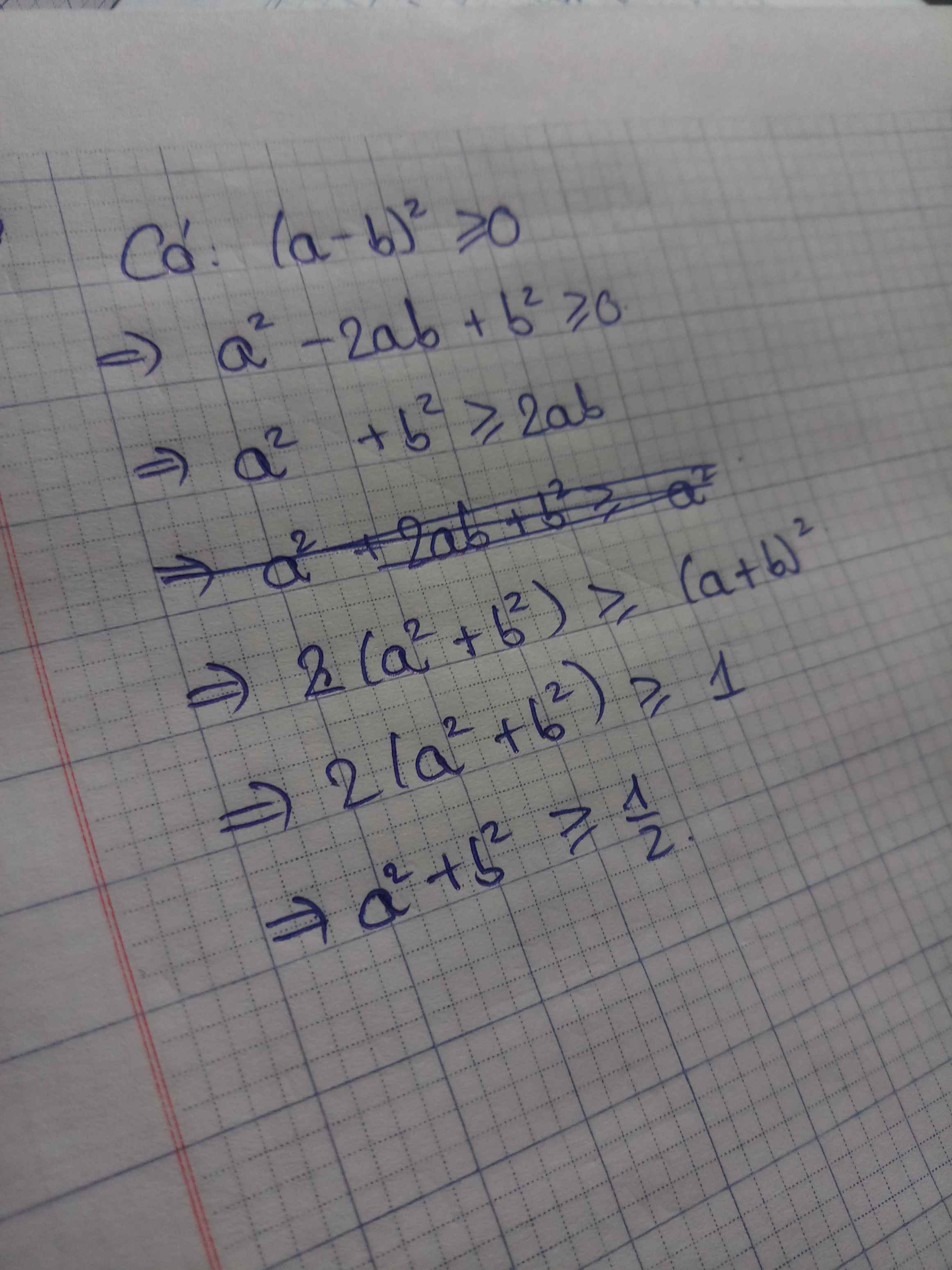
2 ) đề sai rùi bạn ơi ! Mk giải theo đề đúng nka !!
CMR : nếu \(a+b>1\)thì \(a^2+b^2>\frac{1}{2}\)
Ta có : \(a+b>1>0\) ( 1 )
Bình phương hai vế ta được :
\(\left(a+b\right)^2>1\)\(\Leftrightarrow a^2+2ab+b^2>1\) ( 2 )
Mặt khác :
\(\left(a-b\right)^2\ge0\)\(\Leftrightarrow a^2-2ab+b^2\ge0\) ( 3 )
Cộng từng vế của (2) và (3) , ta được:
\(2a^2+2b^2>1\)\(\Leftrightarrow2\left(a^2+b^2\right)>1\)\(\Leftrightarrow a^2+b^2>\frac{1}{2}\left(dpcm\right)\)
tk cko mk nka vì công ngồi đánh máy tình !!!
3 tháng 5 2017
Biết \(a>b\)và \(b>2\)\(\Leftrightarrow a>2\)
Ta có : \(a>2\)
\(\Leftrightarrow-3a< -6\)( Nhân 2 vế với -3 bất đẳng thức đổi chiều )
\(\Leftrightarrow-3a+6< 0\)(Cộng 2 vế với 6)
\(\Leftrightarrowđpcm\)
tk nka !1
20 tháng 6 2018
a \(2a>b;2a>0\Rightarrow2a+2a>b+0\Rightarrow4a>b\)
b \(4a^2+b^2=5ab\Rightarrow4a^2+b^2-5ab=0\Rightarrow\left(4a^2-4ab\right)-\left(ab-b^2\right)=0\)
\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\Rightarrow\left(4a-b\right)\left(a-b\right)=0\Rightarrow\hept{\begin{cases}4a-b=0\Rightarrow4a=b\\a-b=0\Rightarrow a=b\end{cases}}\)
TV
8
2 tháng 5 2016
Với mọi a, b ta có :
( a - b) 2 >= 0
<=> a2 - 2ab + b2 >= 0
<=> a2 + b2 >=2ab
<=> 2 ( a2 + b2 ) >= a2 +2ab + b2
<=> 2 (a2 + b2 ) >= ( a + b )2 mà a+b=1 nên 2 ( a2 + b2 ) >=1
<=> a2 + b2 >= 1/2
Dấu “ = " xảy ra khi và chỉ khi : a=b mà a+b=1 nên a=b=1/2
VN
2 tháng 5 2016
Với mọi a, b ta có :
( a - b) 2 >= 0
<=> a2 - 2ab + b2 >= 0
<=> a2 + b2 >=2ab
<=> 2 ( a2 + b2 ) >= a2 +2ab + b2
<=> 2 (a2 + b2 ) >= ( a + b )2 mà a+b=1 nên 2 ( a2 + b2 ) >=1
<=> a2 + b2 >= 1/2
Dấu “ = " xảy ra khi và chỉ khi : a=b mà a+b=1 nên a=b=1/2
CN
3
M
13 tháng 4 2017
Với mọi a, b ta có :
( a - b) ² >= 0
<=> a² - 2ab + b² >= 0
<=> a² + b² >=2ab
<=> 2 ( a² + b² ) >= a² +2ab + b²
<=> 2 (a² + b² ) >= ( a + b )² mà a+b=1 nên 2 ( a² + b² ) >=1
<=> a² + b² >= 1/2
Dấu “ = " xảy ra khi và chỉ khi : a=b mà a+b=1 nên a=b=1/2
nha!!!
13 tháng 4 2017
Ta có:
\(\left(a-b\right)^2\ge0\)
\(\Leftrightarrow a^2+b^2-2ab\ge0\)
\(\Leftrightarrow a^2+b^2\ge2ab\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge a^2+b^2+2ab\)
\(\Leftrightarrow2\left(a^2+b^2\right)\ge\left(a+b\right)^2=1\)(Vì a+b=1)
\(\Leftrightarrow a^2+b^2\ge\frac{1}{2}\)(Chia 2 vế cho 2)
Dấu '=' xảy ra khi a=b=1/2
NT
0
MT
0