Vẽ lại hình 11 và nói rõ trình tự vẽ hình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


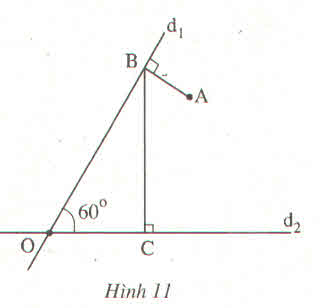
vẽ góc d1Od2 bằng 60 độ
lấy A bất kì nằm trong góc d1Od2
kẻ AB vuông góc với d1O tại B
từ B kẻ BC vuông góc với Od2 tại C

Cách vẽ: Vẽ đường thẳng d1 và d2 cắt nhau tại O sao cho \(\widehat{d_1Od_2=60^0}\).Vẽ A nằm trong \(\widehat{d_1}Od_2\) .Qua A ,vẽ đoạn thẳng AB vuông góc với đường thẳng d1 tại điểm B. Qua B, vẽ đoạn thẳng BC vuông góc với đường thẳng d2 tại C.


Vẽ đường thẳng d1 và đường thẳng d2 ; 2 đường thẳng này cắt nhau tại O tạo thành một góc \(\widehat{d_1Od_2}=60^o\)
Lấy một điểm A nằm trong góc d1Od2; hạ đường vuông góc từ A đến d1, cắt d1 tại B. Từ B lại hạ đường vuông góc đến d2, cắt d2 tại C
Cảm ơn bn rất nhiều nhưng nếu sai thì cho rút lại lời cảm ơn hehe

- Dùng thước thẳng vẽ d
- Lấy điểm O trên d
- Dùng êke vẽ d' vuông góc với d tại O
- Dùng thước thẳng vẽ d
- Lấy điểm O ngoài d
- Dùng êke vẽ d' qua O vuông góc với d

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)
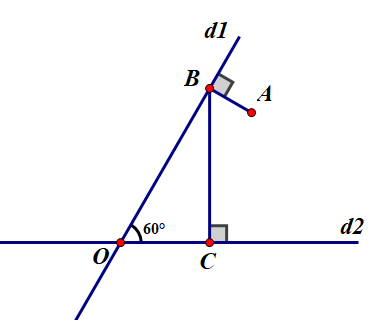


Vẽ đường thẳng d2 bất kì. Lấy điểm O nằm trên d2.
Vẽ đường thẳng d1 cắt d2 tại O và tạo với d2 góc 60º.
Lấy điểm A tùy ý nằm trong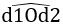
Vẽ đoạn thẳng AB vuông góc với d1 tại B
Vẽ đoạn thẳng BC vuông góc với d2 tại C.