Mn giải giúp mik câu 2 và phần b câu 3 với ạ . Cảm ơn mn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
BD
1
Những câu hỏi liên quan
N
3
9 tháng 9 2021
1.
a.\(n_{HCl}=0,2.0,15=0,03\left(mol\right)\)
b.\(n_{H_2}=\dfrac{11,2}{22,4}=0,5\left(mol\right)\)
c.\(n_{H_2SO_4}=\dfrac{4,9}{98}=0,05\left(mol\right)\)
d.\(m_{H_2SO_4}=10\%.9,8=0,98\left(g\right)\Rightarrow n_{H_2SO_4}=\dfrac{0,98}{98}=0,01\left(mol\right)\)
e.\(m_{NaOH}=6.5\%=0,3\left(g\right)\Rightarrow n_{NaOH}=\dfrac{0,3}{40}=0,0075\left(mol\right)\)
f.\(m_{ddNaOH}=125.1,2=150\left(g\right)\Rightarrow m_{NaOH}=150.20\%=30\left(g\right)\)
\(\Rightarrow n_{NaOH}=\dfrac{30}{40}=0,75\left(mol\right)\)
9 tháng 9 2021
2.
\(m_{NaOH}=10.20\%=2\left(g\right)\Rightarrow n_{NaOH}=\dfrac{2}{40}=0,05\left(mol\right)\)
PTHH: 2NaOH + H2SO4 → Na2SO4 + H2O
Mol: 0,05 0,025
\(\Rightarrow m_{Na_2SO_4}=0,025.142=3,55\left(g\right)\)
3.
\(n_{NaCl}=\dfrac{5,85}{58,5}=0,1\left(mol\right)\)
PTHH: 2NaCl + 2H2O → 2NaOH + Cl2 + H2
Mol: 0,1 0,1
\(m_{NaOH}=0,1.40=4\left(g\right)\Rightarrow m_{ddNaOH}=\dfrac{4.100\%}{5\%}=80\left(g\right)\)
\(\Rightarrow V_{ddNaOH}=\dfrac{80}{1,2}=66,7\left(ml\right)\)
S
Mn ơi, giải hộ mik câu này với! Tối nay mik phải nộp rồi ạ! Cảm ơn mn nhiều lắm!
2
12 tháng 9 2021
f: \(3ab-6a+b-2\)
\(=3a\left(b-2\right)+\left(b-2\right)\)
\(=\left(b-2\right)\left(3a+1\right)\)
QN
0
20 tháng 6 2023
1:
AC=căn 5^2-3^2=4cm
BH=AB^2/BC=1,8cm
CH=5-1,8=3,2cm
AH=3*4/5=2,4cm
2:
ΔCBA vuông tại B có tan 40=BC/BA
=>BC/10=tan40
=>BC=8,39(m)
ΔCBD vuông tại B có tan D=BC/BD
=>BD=8,39/tan35=11,98(m)
5 tháng 7 2021
Đk:\(y^2-2x-5y+6\ge0\)
Pt (1)\(\Leftrightarrow\left(x^2-1\right)-\left(xy-y\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+1\right)-y\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2-y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=x+2\end{matrix}\right.\)
TH1: Thay x=1 vào pt (2) ta đc: \(3\sqrt{y^2-5y+4}=y+9\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+9\ge0\\9\left(x^2-5y+4\right)=y^2+18y+81\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y\ge-9\\8y^2-63y-45=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}y=\dfrac{63+3\sqrt{601}}{16}\\y=\dfrac{63-3\sqrt{601}}{16}\end{matrix}\right.\) (tm)
TH2: Thay y=x+2 vào pt (2) ta đc:
\(\left(x-1\right)^2+3\sqrt{\left(x+2\right)^2-2x-5\left(x+2\right)+6}=x+2+9\)
\(\Leftrightarrow x^2-3x-10+3\sqrt{x^2-3x}=0\)
Đặt \(t=\sqrt{x^2-3x}\left(t\ge0\right)\)
Pttt: \(t^2-10+3t=0\)\(\Leftrightarrow\left[{}\begin{matrix}t=2\left(tm\right)\\t=-5\left(ktm\right)\end{matrix}\right.\)
\(\Rightarrow2=\sqrt{x^2-3x}\)\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-1\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}y=6\\y=1\end{matrix}\right.\) (tm)
Vậy \(\left(x;y\right)=\text{}\left\{\left(1;\dfrac{63+3\sqrt{601}}{16}\right);\left(1;\dfrac{63-3\sqrt{601}}{16}\right),\left(4;6\right),\left(-1;1\right)\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 7 2021
Xét pt đầu:
\(\left(x^2+x-2\right)-y\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2\right)-y\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x+2-y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\y=x+2\end{matrix}\right.\)
- Với \(x=1\) thay xuống pt dưới:
\(3\sqrt{y^2-5y+4}=y+9\) \(\left(y\ge-9\right)\)
\(\Leftrightarrow9\left(y^2-5y+4\right)=y^2+18y+81\)
\(\Leftrightarrow8y^2-63y-45=0\)
\(\Rightarrow y=\dfrac{63\pm3\sqrt{601}}{16}\) (thỏa mãn)
- Với \(y=x+2\) thay xuống pt dưới:
\(\left(x-1\right)^2+3\sqrt{x^2-3x}=x+11\) (ĐKXĐ: ....)
\(\Leftrightarrow x^2-3x+3\sqrt{x^2-3x}-10=0\)
Đặt \(\sqrt{x^2-3x}=t\ge0\)
\(\Rightarrow t^2+3t-10=0\Rightarrow\left[{}\begin{matrix}t=2\\t=-5\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow\sqrt{x^2-3x}=2\Leftrightarrow x^2-3x-4=0\)
\(\Leftrightarrow...\)
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
4 tháng 2 2022
Bài 9:
\(\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{-3}=\dfrac{z}{-17}=\dfrac{t}{9}=-2\)
=>x=-10; y=6; z=34; t=-18
Bài 10:
\(\Leftrightarrow\dfrac{8}{x}=\dfrac{y}{21}=\dfrac{40}{z}=\dfrac{16}{t}=\dfrac{u}{111}=\dfrac{4}{3}\)
=>x=6; y=28; z=30; t=12; u=148
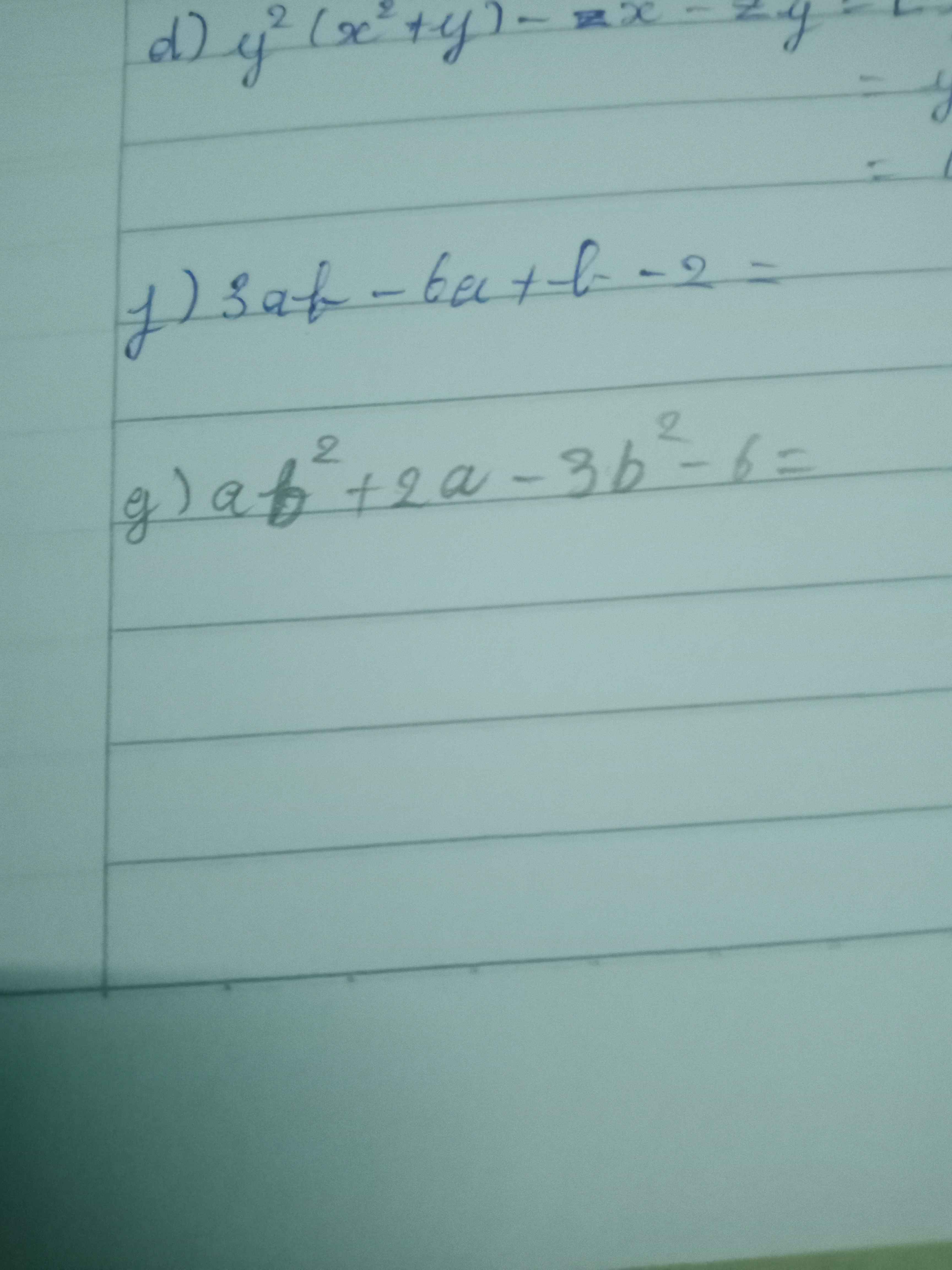
Câu 2:
Ta có: \(x^2-2\left(m+1\right)x+m^2+4=0\)
a=1; b=-2m-2; \(c=m^2+4\)
\(\text{Δ}=b^2-4ac\)
\(=\left(-2m-2\right)^2-4\cdot\left(m^2+4\right)\)
\(=4m^2+8m+4-4m^2-16\)
=8m-12
Để phương trình có hai nghiệm phân biệt thì Δ>0
\(\Leftrightarrow8m>12\)
hay \(m>\dfrac{3}{2}\)
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)=2m+2\\x_1x_2=m^2+4\end{matrix}\right.\)
Vì x1 là nghiệm của phương trình nên ta có:
\(x_1^2-2\left(m+1\right)\cdot x_1+m^2+4=0\)
\(\Leftrightarrow x_1^2=2\left(m+1\right)x_1-m^2-4\)
Ta có: \(x_1^2+2\left(m+1\right)x_2=2m^2+20\)
\(\Leftrightarrow2\left(m+1\right)x_1-m^2-4+2\left(m+1\right)x_2-2m^2-20=0\)
\(\Leftrightarrow2\left(m+1\right)\left(x_1+x_2\right)-3m^2-24=0\)
\(\Leftrightarrow2\left(m+1\right)\cdot\left(2m+2\right)-3m^2-24=0\)
\(\Leftrightarrow4m^2+8m+4-3m^2-24=0\)
\(\Leftrightarrow m^2+8m-20=0\)
Đến đây bạn tự tìm m là xong rồi
Cảm ơn b nha