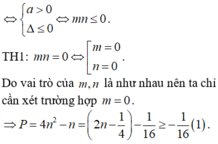cho biểu thức P = m2(m2-n)(m3-n6)(m+n2)giá trị của P khi m=16 n= -4 là...........
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1 2021
a) Ta có: \(A=-34x+34y\)
\(=-34\left(x-y\right)\)
Thay x-y=2 vào biểu thức A=-34(x-y), ta được:
\(A=-34\cdot2=-68\)
Vậy: Khi x-y=2 thì A=68
b) Ta có: \(B=ax-ay+bx-by\)
\(=a\left(x-y\right)+b\left(x-y\right)\)
\(=\left(x-y\right)\left(a+b\right)\)
Thay a+b=-7 và x-y=-1 vào biểu thức \(B=\left(x-y\right)\left(a+b\right)\), ta được:
\(B=-1\cdot\left(-7\right)=7\)
Vậy: Khi a+b=-7 và x-y=-1 thì B=7
3 tháng 10 2021
a: \(A=2\left(m^3+n^3\right)-3\left(m^2+n^2\right)\)
\(=2\left[\left(m+n\right)^3-3mn\left(m+n\right)\right]-3\left[\left(m+n\right)^2-2mn\right]\)
\(=2-6mn-3+6mn\)
=-1
c: \(C=\left(a-1\right)^3-4a\left(a+1\right)\left(a-1\right)+3\left(a-1\right)\left(a^2+a+1\right)\)
\(=a^3-3a^2+3a-1-4a\left(a^2-1\right)+3a^3-3\)
\(=4a^3-3a^2+3a-4-4a^3+4a\)
\(=-3a^2+7a-4\)
\(=-3\cdot9-21-4\)
=-27-21-4
=-52
19 tháng 12 2020
Ta có \(xy\le\dfrac{\left(x+y\right)^2}{4}\).
Do đó ta có: \(x+y+xy=x+y-2xy+3xy\le x+y-2xy+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Rightarrow x^2+y^2\le x+y-2xy+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Leftrightarrow\dfrac{1}{4}\left(x+y\right)^2-\left(x+y\right)\le0\)
\(\Leftrightarrow\left(x+y\right)\left[\dfrac{1}{4}\left(x+y\right)-1\right]\le0\)
\(\Leftrightarrow0\le x+y\le4\).
Do đó m = 0, n = 4.
Vậy m2 + n2 = 16. Chọn A.
2
6 tháng 1 2023
Thay hai điểm `(\sqrt{2};m)` và `(-\sqrt{3};n)` vào `y=x^2` ta có:
`{(m=(\sqrt{2})^2),(n=(-\sqrt{3})^2):}<=>{(m^2=4),(n^2=9):}`
`=>m^2-n^2=4-9=-5`
`->bb D`
