Bài 13. (*) Cho ∆𝐴𝐵𝐶 nhọn có AM là đường trung tuyến. Gọi O là trung điểm AM. Qua O
vẽ đường thẳng d cắt các cạnh AB, AC. Gọi D, E, F lần lượt là chân đường vuông góc kẻ từ
B, A, C đến đường thẳng d. Chứng minh: AE = 𝐵𝐷+𝐶𝐹
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 11 2017
Ta có: BB’ ⊥ d (gt)
CC’ ⊥ d (gt)
Suy ra: BB’ // CC’
Tứ giác BB’CC’ là hình thang
Kẻ MM’ ⊥ d
⇒ MM’ // BB’ // CC’
Nên MM’ là đường trung bình của hình thang BB’CC’
⇒MM′=BB′+CC′2(1)⇒MM′=BB′+CC′2(1)
Xét hai tam giác vuông AA’O và MM’O:
ˆOA′A=ˆOM′MOA′A^=OM′M^
AO = MO (gt)
ˆAOA′=ˆMOM′AOA′^=MOM′^ (đối đỉnh)
Do đó: ∆ AA’O = ∆ MM’O (cạnh huyền, góc nhọn)
⇒ AA’ = MM’ (2)
Từ (1) và (2) suy ra: AA′=BB′+CC′2AA′=BB′+CC′/2.
CM
1 tháng 4 2019
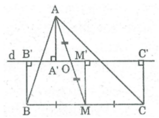
Ta có: BB' ⊥ d (gt)
CC' ⊥ d (gt)
Suy ra: BB'// CC'
Tứ giác BB'C'C là hình thang
Kẻ MM' ⊥ d ⇒ MM' // BB' // CC'
Lại có M là trung điểm của BC nên M' là trung điểm của B’C’
⇒ MM' là đường trung bình của hình thang BB'C'C
⇒ MM' = (BB' + CC') / 2 (1)
* Xét hai tam giác vuông AA'O và MM'O:
∠ (AA'O) = ∠ (MM' O) = 90 0
AO=MO (gt)
∠ (AOA') = ∠ (MOM' ) (2 góc đối đỉnh)
Do đó: ∆ AA'O = ∆ MM'O (cạnh huyền, cạnh góc nhọn)
⇒AA' = MM' (2)
Từ (1) và (2) suy ra: AA' = (BB' + CC') / 2
1 tháng 1 2018
a) ta có AM=MD (gt)
BM=MC (AM là trung tuyến của tam giác)
Mà AD cắt BC tai M
=> ABCD là hình bình hành
Mà \(\widehat{BAC}=90^{\sigma}\) (gt)
=> ABCD là hình chữ nhật
b) ta có \(BI\perp AD\) (gt)
lại có \(CK\perp AD\) (gt)
=> BI // CK
bn coi lại câu c có sai đề k, nếu đúng thì mk chỉ lm đc 2 câu trên thôi!
Chọn mk nha
S
2 tháng 9 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)