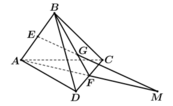
Cho tứ diện ABCD. Gọi E, F lần lượt là trung điểm của AB và CD. G là trọng tâm của tam giác BCD. Tìm giao điểm của EG với (ACD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



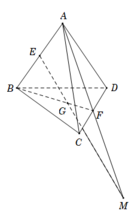
Vì G là trọng tâm tam giác BCD và F là trung điểm của CD nên G thuộc (ABF)
Ta có E là trung điểm của AB nên E thuộc ( ABF).
Gọi M là giao điểm của EG và AF mà A F ⊂ A C D suy ra M thuộc (ACD).
Vậy giao điểm của EG và mp (ACD) là giao điểm M của EG và AF
Chọn B.

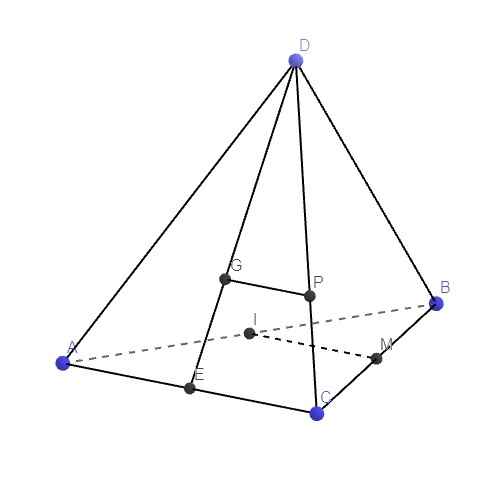
Gọi E là trung điểm AC, do G là trọng tâm tam giác ACD \(\Rightarrow G\in DE\)
Theo t/c trọng tâm: \(\dfrac{GE}{GD}=\dfrac{1}{2}\)
Do I là trung điểm AB, M là trung điểm BC \(\Rightarrow\) IM là đường trung bình tam giác ABC
\(\Rightarrow IM||AC\)
Qua G kẻ đường thẳng song song AC cắt CD tại P
\(\left\{{}\begin{matrix}G\in\left(IGM\right)\\GP||AC||IM\end{matrix}\right.\) \(\Rightarrow P\in\left(IGM\right)\)
\(\Rightarrow P=CD\cap\left(IGM\right)\)
Theo định lý Talet: \(\dfrac{PC}{PD}=\dfrac{GE}{GD}=\dfrac{1}{2}\)

Ta có:
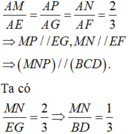
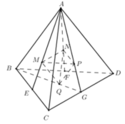
Ta có ∆ M N P đồng dạng với ∆ B C D theo tỉ số
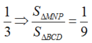
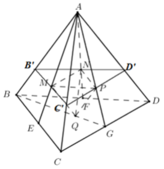
Dựng B ' C ' qua M và song song BC. C ' D ' qua P và song song với CD.
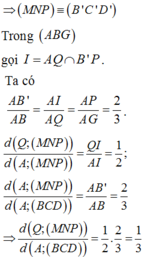

Chọn D.