Tại sao 2 x b x b = 12 x ( 2 x b - b ) lại được 2 x b x b = 12 x b vậy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
10 tháng 1 2024
a) Ta có: \(A = {x^2} + 6{\rm{x}} + 10 = {x^2} + 2.x.3 + {3^2} + 1 = {\left( {x + 3} \right)^2} + 1\)
Thay x = -103 vào biểu thức A rút gọn ta được:
\(A = {\left( { - 103 + 3} \right)^2} + 1 = 10000 + 1 = 10001\)
Vậy A = 10001 tại x = - 103
b) Ta có: \(B = {x^3} + 6{{\rm{x}}^2} + 12{\rm{x}} + 12 = {x^3} + 3.{x^2}.2 + 3.x{.2^2} + {2^3} + 4 = {\left( {x + 2} \right)^3} + 4\)
Thay x = 8 vào biểu thức B vừa rút gọn ta được:
\(B = {\left( {8 + 2} \right)^3} + 4 = {10^3} + 4 = 1004\)
Vậy B = 1004 tại x = 8
CM
23 tháng 8 2019
a) Vì x ∈ B (5) nên x ∈ {0;5;10;15;20;25;30;35;40;...}.
Mặt khác 20 ≤ x ≤ 36 => x ∈ {20; 25; 30; 35).
b) Ta có Ư(12) = {1;2;3;4;6;12}. Vì x ∈ Ư (12) và 2 ≤ x ≤ 8
nên x ∈ {2; 3; 4; 6}.
c) Tương tự câu a), ta có:
x ∈ {15; 20; 25; 30; 35; 40; 45; 50; 55; 60; 65; 70; 75).
d) Tương tự câu b), ta có x ∈ {6;12}
NP
1
30 tháng 10 2018
A xác định \(\Leftrightarrow x^2-1\ne0\Leftrightarrow x\ne\left\{1;-1\right\}\)
B xác định \(\Leftrightarrow x^3-8\ne0\Leftrightarrow x^3\ne8\Leftrightarrow x\ne2\)
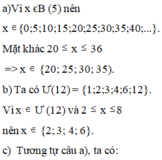
đây: 2xb-b tức là 2xb-1xb đúng ko?