Cho biểu thức A= (1+x^2/x^2+1):(1/x-1-2x/x^3+x-x^2-1)
a) Rút gọn A
b) Tính giá trị của A tại x= -1/2
c)Tìm x để A<1
d) Tìm các giá trị nguyên của x để A có giá trị nguyên
Mình đang cần gấp ak
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 7 2023
a) A=2x2+6x-2x2+3x-4x+6+x-2=6x+4
b) x+1=2 => x=1
Tại x=1, A=6*1+4=10
c) A=6x+4=1/2 => x=(1/2-4)/6=-7/12
H
17 tháng 7 2023
`!`
`a,A=2x(x+3) -(x+2)(2x-3)+x-2`
`= 2x^2 + 6x-(2x^2 -3x+4x-6)+x-2`
`= 2x^2 +6x+2x^2 +3x-4x+6+x-2`
`= (2x^2-2x^2)+(6x+3x-4x+x)+(6-2)`
`=6x+4`
`b, x+1=2`
`=>x=2-1`
`=>x=1`
`A=6x+4` mà `x=1`
Thì `6x+4=6.1+4=10`
`c,` Ta có :
`6x+4=1/2`
`=> 6x=1/2-4`
`=> 6x= -7/2`
`=>x=-7/2 : 6`
`=>x=-7/2 xx1/6`
`=>x= -7/12`
17 tháng 12 2023
a: \(A=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=8x^3-1-7x^3-7=x^3-8\)
b: Thay x=-1/2 vào A, ta được:
\(A=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
18 tháng 12 2023
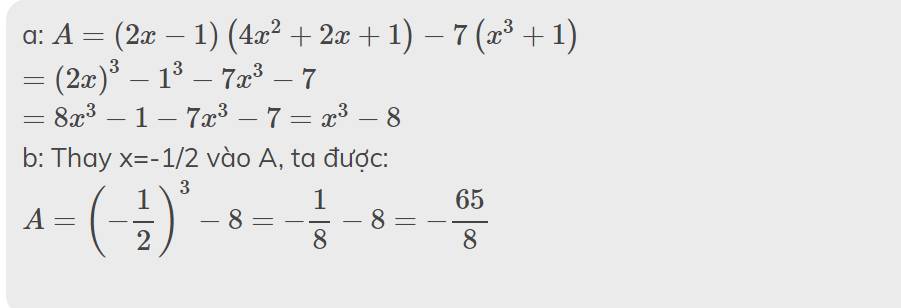
c: \(A=x^3-8=\left(x-2\right)\left(x^2+2x+4\right)\)
Để A là số nguyên tố thì x-2=1
=>x=3
8 tháng 12 2021
a: \(A=\dfrac{x+2+x^2-2x+x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2}{x^2-4}\)
12 tháng 12 2021
a: \(A=\dfrac{x+2+x^2-2x+x-2}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2-2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{x}{x+2}\)
8 tháng 12 2021
a) \(A=\dfrac{x+2+x^2-2x+1}{\left(x-2\right)\left(x+2\right)}=\dfrac{x^2-x+1}{\left(x-2\right)\left(x+2\right)}\)
8 tháng 12 2021
a: \(A=\dfrac{x+2+x^2-2x+x-2}{\left(x+2\right)\left(x-2\right)}=\dfrac{x^2}{x^2-4}\)
4 tháng 2 2021
a) ĐKXĐ: \(x\notin\left\{0;-\dfrac{1}{2};\dfrac{1}{2}\right\}\)
Ta có: \(A=\left(\dfrac{1}{2x-1}+\dfrac{3}{1-4x^2}-\dfrac{2}{2x+1}\right):\left(\dfrac{x^2}{2x^2+x}\right)\)
\(=\left(\dfrac{2x+1}{\left(2x-1\right)\left(2x+1\right)}-\dfrac{3}{\left(2x-1\right)\left(2x+1\right)}-\dfrac{2\left(2x-1\right)}{\left(2x+1\right)\left(2x-1\right)}\right):\left(\dfrac{x^2}{x\left(2x+1\right)}\right)\)
\(=\dfrac{2x+1-3-4x+2}{\left(2x-1\right)\left(2x+1\right)}:\dfrac{x}{2x+1}\)
\(=\dfrac{-2x}{\left(2x-1\right)\left(2x+1\right)}\cdot\dfrac{2x+1}{x}\)
\(=\dfrac{-2}{2x-1}\)
b) Ta có: \(\left|2x-1\right|=2\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-1=2\\2x-1=-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\2x=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\left(nhận\right)\\x=-\dfrac{1}{2}\left(loại\right)\end{matrix}\right.\)
Thay \(x=\dfrac{3}{2}\) vào biểu thức \(A=\dfrac{-2}{2x-1}\), ta được:
\(A=-2:\left(2\cdot\dfrac{3}{2}-1\right)=-2:\left(3-1\right)=-2:2=-1\)
Vậy: Khi \(\left|2x-1\right|=2\) thì A=-1
c) Để \(A=\dfrac{1}{3}\) thì \(\dfrac{-2}{2x-1}=\dfrac{1}{3}\)
\(\Leftrightarrow2x-1=-6\)
\(\Leftrightarrow2x=-5\)
hay \(x=-\dfrac{5}{2}\)(thỏa ĐK)
Vậy: Để \(A=\dfrac{1}{3}\) thì \(x=-\dfrac{5}{2}\)
TM
26 tháng 1 2022
1. ĐKXĐ: \(x\ne\pm1\)
2. \(A=\left(\dfrac{x+1}{x-1}-\dfrac{x+3}{x+1}\right)\cdot\dfrac{x+1}{2}\)
\(=\dfrac{\left(x+1\right)^2-\left(x-3\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{x^2+2x+1-x^2+4x-3}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{6x-2}{\left(x-1\right)\left(x+1\right)}\cdot\dfrac{x+1}{2}\)
\(=\dfrac{2\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x+1\right)}\)
\(=\dfrac{x-3}{x-1}\)
3. Tại x = 5, A có giá trị là:
\(\dfrac{5-3}{5-1}=\dfrac{1}{2}\)
4. \(A=\dfrac{x-3}{x-1}\) \(=\dfrac{x-1-3}{x-1}=1-\dfrac{3}{x-1}\)
Để A nguyên => \(3⋮\left(x-1\right)\) hay \(\left(x-1\right)\inƯ\left(3\right)=\left\{1;-1;3;-3\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=1\\x-1=-1\\x-1=3\\x-1=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=2\left(tmđk\right)\\x=0\left(tmđk\right)\\x=4\left(tmđk\right)\\x=-2\left(tmđk\right)\end{matrix}\right.\)
Vậy: A nguyên khi \(x=\left\{2;0;4;-2\right\}\)
a) Ta có: \(A=\left(1+\dfrac{x^2}{x^2+1}\right):\left(\dfrac{1}{x-1}-\dfrac{2x}{x^3+x-x^2-1}\right)\)
\(=\dfrac{2x^2+1}{x^2+1}:\dfrac{x^2+1-2x}{\left(x-1\right)\left(x^2+1\right)}\)
\(=\dfrac{2x^2+1}{x^2+1}\cdot\dfrac{\left(x-1\right)\left(x^2+1\right)}{\left(x-1\right)^2}\)
\(=\dfrac{2x^2+1}{x-1}\)
b) Thay \(x=-\dfrac{1}{2}\) vào A, ta được:
\(A=\left(2\cdot\dfrac{1}{4}+1\right):\left(\dfrac{-1}{2}-1\right)\)
\(=\dfrac{3}{2}:\dfrac{-3}{2}=-1\)
c) Để A<1 thì A-1<0
\(\Leftrightarrow\dfrac{2x^2+1}{x-1}-1< 0\)
\(\Leftrightarrow\dfrac{2x^2+1-x+1}{x-1}< 0\)
\(\Leftrightarrow\dfrac{2x^2-x+2}{x-1}< 0\)
\(\Leftrightarrow x-1< 0\)
hay x<1
câu c xét hiệu à bạn