Có hai bình cách nhiệt. Bình 1 chứa 4kg nước ở 20 độ C. Bình 2 chứa 8kg nước ở 40 độ C. Người ta trút 1 lượng nước m từ bình 2 sang bình 1. Sau khi nhiệt độ ở bình 1 đã ổn định người ta lại trút 1 lượ...

TN

Thảo Nguyễn

18 tháng 7 2021

Có hai bình cách nhiệt. Bình 1 chứa 4kg nước ở 20 độ C. Bình 2 chứa 8kg nước ở 40 độ C. Người ta trút 1 lượng nước m từ bình 2 sang bình 1. Sau khi nhiệt độ ở bình 1 đã ổn định người ta lại trút 1 lượng nước m từ bình 1 sang bình 2. Nhiệt độ ở bình 2 khi đã cân bằng nhiệt là 38 độ C. Tính lượng nước m đã trút và nhiệt độ ổn định ở bình...

Đọc tiếp

#Vật lý lớp 8

1

DK

Dang Khoa ~xh

18 tháng 7 2021

THAM KHẢO!

Đúng(1)

KD

Khang Diệp Lục

18 tháng 7 2021

Còn nhiều người làm được bài này, không khiến bạn copy rồi ghi tham khảo nhé!

Muốn ghi tham khảo qua box Xã Hội chơi ;)

Đúng(1)

LT

Lê Thị Thu Uyên

5 tháng 5 2022

Có 2 bình cách nhiệ, bình 1 chứa 4kg nước ở nhiệt độ 20 độ c.Bình 2 chứa 8kg nước ở 40 độ c.Người ta trút một lượng nước (m) từ bình 2 sang bình 1.Sau khi nhiệt độ ở bình đã ổn định , người ta lại trút một lượng nước (m) từ bình 1 vào bình 2.Nhiệt độ ở bình 2 sau khi ổn định là 38 độ c.Hãy tính lượng nước (m)đã trút trong mỗi lần và nhiệt độ ở bình 1 sau lần đổ thứ...

Đọc tiếp

#Vật lý lớp 8

2

TT

Trần Tuấn Hoàng

5 tháng 5 2022

*Khi trút trong lần 1:

-Nhiệt lượng nước ở bình 1 lúc đầu thu vào là:

$Q_{thu_1}=m_1.c.\left(t-t_1\right)=4.4200.\left(t-20\right)=16800.\left(t-20\right)\left(J\right)$.

-Nhiệt lượng nước trút từ bình 2 sang bình 1 tỏa ra là:

$Q_{tỏa_1}=m.c.\left(t_2-t\right)=4200m.\left(40-t\right)=\left(J\right)$

-Bỏ qua sự mất mát nhiệt, ta có phương trình cân bằng nhiệt:

$Q_{thu_1}=Q_{tỏa_1}$

$\Leftrightarrow16800\left(t-20\right)=4200m\left(40-t\right)$

$\Leftrightarrow16800t-336000=168000m-4200t$

$\Leftrightarrow21000t=504000m$

$\Leftrightarrow t=24m\left(^oC\right)$.

*Lần 2:

-Vì nhiệt độ cân bằng lần 2 là 38^oC nên nước ở bình 2 lúc đó tỏa nhiệt, còn lượng nước trút lần 2 thu nhiệt.

-Lượng nước ở bình 2 sau lần đầu trút là:

$m_2'=m_2-m=8-m\left(kg\right)$

-Nhiệt lượng nước trút từ bình 1 sang bình 2 thu vào là:

$Q_{thu_2}=m.c.\left(t'-t\right)=4200m.\left(38-24m\right)\left(J\right)$

-Nhiệt lượng nước ở bình 2 sau lần đầu trút tỏa ra là:

$Q_{tỏa_2}=m_2'.c.\left(t_2-t'\right)=\left(8-m\right).4200.\left(40-38\right)=8400\left(8-m\right)\left(J\right)$

-Bỏ qua sự mất mát nhiệt, ta có phương trình cân bằng nhiệt:

$Q_{thu_2}=Q_{tỏa_2}$

$\Leftrightarrow4200m.\left(38-24m\right)=8400\left(8-m\right)$

$\Leftrightarrow159600m-100800m^2=67200-8400m$

$\Leftrightarrow168000m-100800m^2-67200=0$

$\Leftrightarrow\left[{}\begin{matrix}m=1\left(nhận\right)\\m=\dfrac{2}{3}\left(loại\right)\end{matrix}\right.$

$\Rightarrow$Lượng nước đã trút trong mỗi lần là: $m=1\left(kg\right)$ và nhiệt độ ở bình 1 sau lần đổ thứ nhất là: $t=24m=24.1=24^oC$

Đúng(1)

TT

Trần Tuấn Hoàng

5 tháng 5 2022

Đúng(0)

LK

Lí Khó

26 tháng 8 2016

Có 2 bình cách nhiệt , bình 1 chứa 4 kg nước ở nhiệt độ 20 độ C.bình 2 chứa 8kg nước ở 40 độ C người ta rút một lượng nước m từ bình 2 sang bình 1.Sau khi nhiệt độ ở bình 1 đã ổn định người ta lại trút lượng nước m từ bình 1 vào bình 2.nhiệt độ ở bình 2 sau khi ổn định là 38 độ C. hãy tính lượng nước đã trút trong mỗi lần và nhiệt độ ở bình 1 sau lần đổ thứ...

Đọc tiếp

#Vật lý lớp 8

2

VD

Võ Đông Anh Tuấn

26 tháng 8 2016

undefined

Đúng(1)

HT

Hà thúy anh

26 tháng 8 2016

Gọi t lả nhiệt độ sau lần 1.
Khi đổ lượng nước m vào bình 1 ta có pt:
Qthu=Qtoả
m.c.(40-t)= 4.c.(t-20)
<=> 40m-mt=4t-80 (1)
Khi đổ m lại bình 2 ta có pt:
Qthu=Qtoả
(8-m).c.(40-38)= m.c.(38-t)
16-2m= 38m-mt
<=> 16= 40m-mt (2)
Từ (1),(2):
=>4t-80= 16
=> t= 24.
Vậy nhiệt độ sau cân bằng 1 là 24 độ C.
Lượng nước m là:
16=40m-24m= 16m
=> m= 1 (kg)

Đúng(0)

DN

Dieu Ngo

5 tháng 11 2016

Mn giúp mk vs, cần gấp nha!!!Có 2 bình cách nhiệt . Bình 1 chứa m=4kg nước ở nhiệt độ t1=20°C. Bình 2 chứa m2=8kg nước ở nhiệt độ t2=40°C. Người ta trút 1 lượng nước m từ bình 2 sang bình 1. Sau khi nhiệt độ ở bình 1 đã ổn định, người ta lại trút lượng nước m từ bình 1 sang bình 2. Nhiệt độ ở bình 2 khi cân bằng nhiệt là t2=38°C. Hãy tính lượng nước m đã trút trong mỗi lần và...

Đọc tiếp

#Vật lý lớp 9

1

TV

Truong Vu Xuan

5 tháng 11 2016

ta có:

lúc đổ từ bình hai sang bình một thì phương trình cân bằng nhiệt là:

Q₁=Q₂

$\Leftrightarrow m_1C\left(t-t_1\right)=mC\left(t_2-t\right)$

$\Leftrightarrow4\left(t-20\right)=m\left(40-t\right)$

$\Leftrightarrow4t-80=40m-mt$

$\Leftrightarrow4t+mt=40m+80$

$\Rightarrow t=\frac{40m+80}{4+m}\left(1\right)$

ta lại có:

lúc trút từ bình 1 sang bình hai thì phương trình cân bằng nhiệt là:

Q₁=Q₂

$\Leftrightarrow mC\left(t'-t\right)=\left(m_2-m\right)C\left(t_2-t'\right)$

$\Leftrightarrow m\left(38-t\right)=\left(8-m\right)\left(40-38\right)$

$\Leftrightarrow m\left(38-\frac{40m+80}{m+4}\right)=2\left(8-m\right)$(thế phương trình (1) vào đây

$\Leftrightarrow\frac{m\left(38m+152-40m-80\right)}{m+4}=16-2m$

$\Leftrightarrow m\left(72-2m\right)=\left(16-2m\right)\left(m+4\right)$

$\Leftrightarrow72m-2m^2=16m+64-2m^2-8m$

$\Leftrightarrow72m-2m^2=8m-2m^2+64$

$\Rightarrow64m-64=0$

$\Rightarrow m=1kg$

$\Rightarrow t=24$ độ C

vậy:lượng nước đã trút là 1kg và nhiệt độ ổn định ở bình 1 là 24 độ C

Đúng(1)

1T

10.Hoàng Tiến Đạt

24 tháng 11 2022

không biết đúng k đọc thấy hiểu mới cả trình bày đẹp nx cảm ơn bạn nhìu nha!

Đúng(0)

BK

Bảo Kun

5 tháng 9 2016

Có 2 bình cách nhiệt . Binhg 1 chứa m1=2kg nước ở nhiệt độ t1 = 40 độ C . Bình 2 chứa m2 = 1kg nước ở nhiệt độ t2=20 độ C . Người ta trút một lượng nước m từ bình 1 sang bình 2 . Sau khi ở bình 2 nhiệt độ đã ổn định , lại trút một lượng nước m như thế từ bình 2 sang bình 1 . Nhiệt độ cân bằng ở bình 1 là 38 độ C .Tính khối lượng m trút trong mỗi lân và nhiệt độ cân bằng ở...

Đọc tiếp

#Vật lý lớp 8

2

LN

Lê Nguyên Hạo

5 tháng 9 2016

Khi trút một lượng nước m từ B1 sang B2 thì m kg nước tỏa nhiệt để hạ nhiệt độ từ t1 (t độ đó) xuống t3, m2 kg nước thu nhiệt để tăng nhiệt độ từ t2 đến t3.
Do nhiệt hao phí không đáng kể ( câu này phải lập luận) có phương trình cân bằng nhiệt
Qtỏa = Qthu
<=> m(t1 - t3) = m2(t3 - t2) (đã rút gọn Cn)
<=> m(40- t3) = 1( t3-20)
<=> m= (t3-20)/(40-t3) (*)
Lúc này ở B1 còn (m1-m) kg nước có nhiệt độ t1=40, ở B2 có ( m2+m) kg nước có nhiệt độ t3
Khi trút một lượng nước m từ B2 về B1 thì (m1-m) kg nước tỏa nhiệt để hạ nhiệt độ từ t1 xuống 38 độ, m kg nước thu nhiệt để tăng nhiệt độ từ t3 lên 38 độ.
(lập luận như trên) có phương trình cần bằng nhiệt
Qtỏa = Q thu
<=>(m1-m)(t1-38) = m(38 - t3)
<=>(2-m)2 = m(38-t3)
<=>4-2m = m(38-t3)
<=>m(38 -t3 +2) =4
<=>m= 4/(40 -t3) (~)

Từ (*) và (~) ta có
t3 -20 = 4
<=>t3 = 24
Suy ra nhiệt độ cân bằng ở bình 2 là 24 độ
Thay t3 = 24 độ vào một trong hai phương trình trên sẽ tìm được m = 0.25 kg

Đúng(4)

VD

Võ Đông Anh Tuấn

5 tháng 9 2016

Xét cả quá trình :

Nhiệt lượn bình 1 tỏa ra :

$Q=m_1.C.2=16800J$

Nhiệt lượng này truyền cho bình 2.

$Q=m_2.C.\left(t-20\right)$

Xét lần trút từ bình 1 sang bình 2.

$mC\left(40-24\right)=m_2C\left(24-20\right)$

Tính được $0,66666kg$

Đúng(1)

OG

Ối giời ối giời ôi

4 tháng 8 2020 - olm

Cho hai bình cách nhiệt. Bình một chứa m1 = 4kg nước ở nhiệt độ t1 = 20oC; bình hai chứa m2 = 8kg nước ở nhiệt độ t2 = 40oC. Người ta trút một lượng nước m từ bình hai sang bình một. Sau khi nhiệt độ ở bình một đã cân bằng là t'1, người ta lại trút một lượng nước m từ bình một sang bình hai. Nhiệt độ ở bình hai khi cân bằng là t'2 = 38oC.Hãy tính lượng nước m đã trút trong mỗi lần và...

Đọc tiếp

#Toán lớp 8

1

B

Bellion

4 tháng 8 2020

Bài làm :

Khi trút lượng nước m từ bình hai sang bình một ta có :

Q_tỏa = Q_thu

<=>mc(t₂ – t'₁) = m₁c(t'₁ – t₁)

<=>m(t₂ – t'₁) = m₁(t'₁ – t₁)

<=> m.(40 – t'₁) = 4.(t'₁ – 20)

<=>40m – mt'₁ = 4t'₁ – 80 (1)

Khi trút lượng nước m từ bình một sang bình hai ta có:

Q_thu = Q_tỏa

<=> mc(t'₂ – t'₁) = c(m₂ – m)(t₂ – t'₂)

<=> m (t'₂ – t'₁) = (m₂ – m)(t₂ – t'₂)

<=> 38m – mt'₁ = 16 – 2m

<=>40m - mt'₁ = 16 (2)

Trừ (1) cho (2) theo vế với vế, ta có :

0 = 4t'₁- 96 → t'₁ = 24⁰C

Thay t'₁ = 24⁰C vào (2) ta có: 40m – 24m = 16 => m = 1kg

Chúc bạn học tốt !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!

Đúng(0)

TN

Tiến Nguyễn

27 tháng 2 2021

có 2 bình cách nhiệt , bình1 chưa m1=4kg nước ở nhiệt độ 20'c . Bình 2 chứa m2=8kg nước ở 40'c . Người ta đổ m(kg) từ bình 2 sang bình 1 . Sau khi nhiệt độ ở bình 1 đã ổn định , người ta lại đổ m(kg) từ bình 1 vào bình 2. Nhiệt độ ở bình 2 sau khi ổn định là 38'c . Hãy tính nhiệt độ ở bình 1 sau lần đổ thứ nhất...

Đọc tiếp

#Vật lý lớp 9

1

SI

Shiba Inu

27 tháng 2 2021

* Tham khảo thoy nha :

Khi đổ lượng nước m từ bình 2 sang bình 1, gọi nhiệt độ cân bằng ở bình 1 là t1’. Ta có phương trình cân bằng nhiệt:

mc( t2 – t1’) = m1c ( t1’ – t1 )

<=>m( t2 – t1’ ) = m1(t1’ – t1)

Ta được: t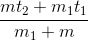1’ = (1)

Khi đổ lượng nước m từ bình 1 sang bình 2, gọi nhiệt độ cân bằng ở bình 2 là t2’. Ta có phương trình cân bằng nhiệt: mc( t2’ – t1’ ) = ( m2 – m )c(t2 – t2’ )

<=> mt2’ – mt1’ = ( m2 – m )( t2 – t2’ )

<=> mt2’ - ( m2 – m )( t2 – t2’ ) = mt1’

Ta được: t1’ = 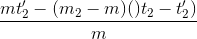(2)

Từ (1) và (2) ta có =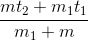

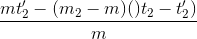
Giải phương trình trên ta được:

m=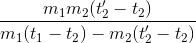= =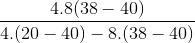1kg

Thay m = 1kg vào (1) ta được: t1’ = 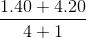= 24oC

Đúng(1)

PQ

Phạm Quỳnh Anh

14 tháng 3 2022

Có hai bình cách nhiệt, bình một chứa m1 = 4 kg nước ở nhiệt độ 20°C. Bình hai chứa m2 = 8 kg nước ở 40°C. Người ta đổ m (kg) từ bình 2 sang bình 1. Sau khi nhiệt độ ở bình 1 đã ổn định, người ta lại đổ m (kg) từ bình 1 vào bình 2. Nhiệt độ ở bình 2 sau khi ổn định là 38°C. Hãy tính nhiệt độ ở bình 1 sau lần đổ thứ nhất...

Đọc tiếp

#Hóa học lớp 8

2

KS

kodo sinichi

14 tháng 3 2022

- Khi đổ một lượng nước m (kg) từ bình 2 sang bình 1. nước ở bình 1 có nhiệt độ cân bằng là t1’.

- Ta có: m.c.(t2 - t1’) = m1c.(t1’- t1)

Hay: m.(t2 - t1’) = m1.(t1’- t1) (1)

- Sau khi đổ m (kg) từ bình 1 sang bình 2 thì nhiệt độ ở bình 2 sau khi cân bằng là t2’ ta lại có:

(m2 - m).c.(t2 - t2’) = m.c(t2’ - t1’)

Hay:

m2t2 - m2t2’ - mt2 + mt2’ = mt2’- mt1’

⇔ m(t2 - t1’) = m2( t2 - t2’) (2)

Hay : 4.(t1’ - 20) = 8.( 40 - 38) ⇔ t1’ = 24

Đúng(1)

TP

Tạ Phương Linh

14 tháng 3 2022

= 24

Đúng(1)

NH

nguyễn huyền diệu

6 tháng 5 2022

có hai bbìn cách nhiệt , bình thứ nhất chứa 2kg nước ở 20 độ c ,bình thứ 2 chứa 4kg nước ở 60 độ c .Người ta rót 1 ca nước từ bình 1 vào bình 2 .Khi bình 2 đã cân bằng nhiệt thì người ta lại rót một ca nước từ bình 2 sang bình 1để lượng nước trong 2 bình như lúc đầu .Nhiệt độ ở bình1 sau khi cân bằng là21,95 độ ca,xác định lượng nước đã rót ở mỗi lần và nhiệt độ cân bằng ở mỗi bìnhb, nếu...

Đọc tiếp

#Vật lý lớp 8

1

C

☆Châuuu~~~(๑╹ω╹๑ )☆

6 tháng 5 2022

Ta có phương trình cân bằng nhiệt ( lần 1)

$Q_{toả_1}=Q_{thu_1}\\ \Leftrightarrow4c\left(60-t_{cb_1}\right)=mc\left(t_{cb_1}-20\right)\\ \Leftrightarrow t_{cb_1}=\dfrac{240+20m}{m+4}\left(1\right)$

Ta có phương trình cân bằng nhiệt ( lần 2 )

$Q_{toả_2}=Q_{thu_2}\\ \Leftrightarrow mc\left(t_{cb_1}-21,95\right)=\left(2-m\right)c.1,95\\ \Leftrightarrow t_{cb_1}=\dfrac{3,9+20m}{m}\left(2\right)$

Từ (1) và (2)

$\Leftrightarrow\dfrac{240+20m}{m+4}=\dfrac{3,9+20m}{m}$

Giải phương trình trên ta được

$\Rightarrow m\approx0,1kg$

Thay m = 0,1kg ta được

$\Leftrightarrow t_{cb}=59^o$

Ta có phương trình cân bằng nhiệt lần 3

$Q_{toả_3}=Q_{thu_3}\\ \Leftrightarrow4c\left(59-t_{cb}\right)=0,1c\left(t_{cb}-21,95\right)\\ \Rightarrow t_{cb}=58,1$

Đúng(2)

HL

hacker lỏ

27 tháng 7 2023

có hai bbìn cách nhiệt , bình thứ nhất chứa 2kg nước ở 20 độ c ,bình thứ 2 chứa 4kg nước ở 60 độ c .Người ta rót 1 ca nước từ bình 1 vào bình 2 .Khi bình 2 đã cân bằng nhiệt thì người ta lại rót một ca nước từ bình 2 sang bình 1để lượng nước trong 2 bình như lúc đầu .Nhiệt độ ở bình1 sau khi cân bằng là21,95 độ ca,xác định lượng nước đã rót ở mỗi lần và nhiệt độ cân bằng ở mỗi bìnhb, nếu...

Đọc tiếp

#Vật lý lớp 8

1

T

trung

28 tháng 7 2023

a/ Giả sử khi rót lượng nước m từ bình 1 sang bình 2, nhiệt độ cân bằng của bình 2 là t nên ta có phương trình cân bằng:

m.(t - t₁) = m₂.(t₂ - t) (1)

Tương tự lần rót tiếp theo nhiệt độ cân bằng ở bình 1 là t' = 21,95⁰C và lượng nước trong bình 1 lúc này chỉ còn (m₁ - m) nên ta có phương trình cân bằng:

m.(t - t') = (m₁ - m).(t' - t₁) (2)

Từ (1) và (2) ta có pt sau:

m₂.(t₂ - t) = m₁.(t' - t₁)

$t = \frac{m_{2} t_{2} (t^{'} - t_{1})}{m_{2}}$ (3)

Thay (3) vào (2) tính toán ta rút phương trình sau:

$m = \frac{m_{1} m_{2} (t^{'} - t_{1})}{m_{2} (t_{2} - t_{1}) - m_{1} (t^{'} - t_{1})}$ (4)

Thay số vào (3) và (4) ta tìm được: t = 59⁰C và m = 0,1 Kg.

b/ Lúc này nhiệt độ của bình 1 và bình 2 lần lượt là 21,95⁰C và 59⁰C bây giờ ta thực hiện rót 0,1Kg nước từ bình 1 sang bình 2 thì ta có thể viết được phương trình sau:

m.(T₂ - t') = m₂.(t - T₂)

$T_{2} = \frac{m_{1} t^{'} + m_{2} t}{m + m_{2}} = 58, 12^{0} C$ ⁰C

Bây giờ ta tiếp tục rót từ bình 2 sang bình 1 ta cũng dễ dàng viết được phương trình sau:

m.(T₁ - T₂) = (m₁ - m).(t - T₁)

$T_{1} = \frac{m T_{2} + (m_{1} - m) t^{'}}{m_{1}} = 23, 76^{o} C$ ⁰C

dấu / là phân số

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP