x : y : z = 1 : 2 : 3 và x\(^3\) + y\(^3\) + 2\(^3\) =36
bạn nào trả lời chi tiết và nhanh nhất mik sẽ tick cho nhé ( mik đang cần gấp)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
DH
Dưa Hấu
17 tháng 7 2021
Đúng(2)
Những câu hỏi liên quan
3 tháng 9 2021
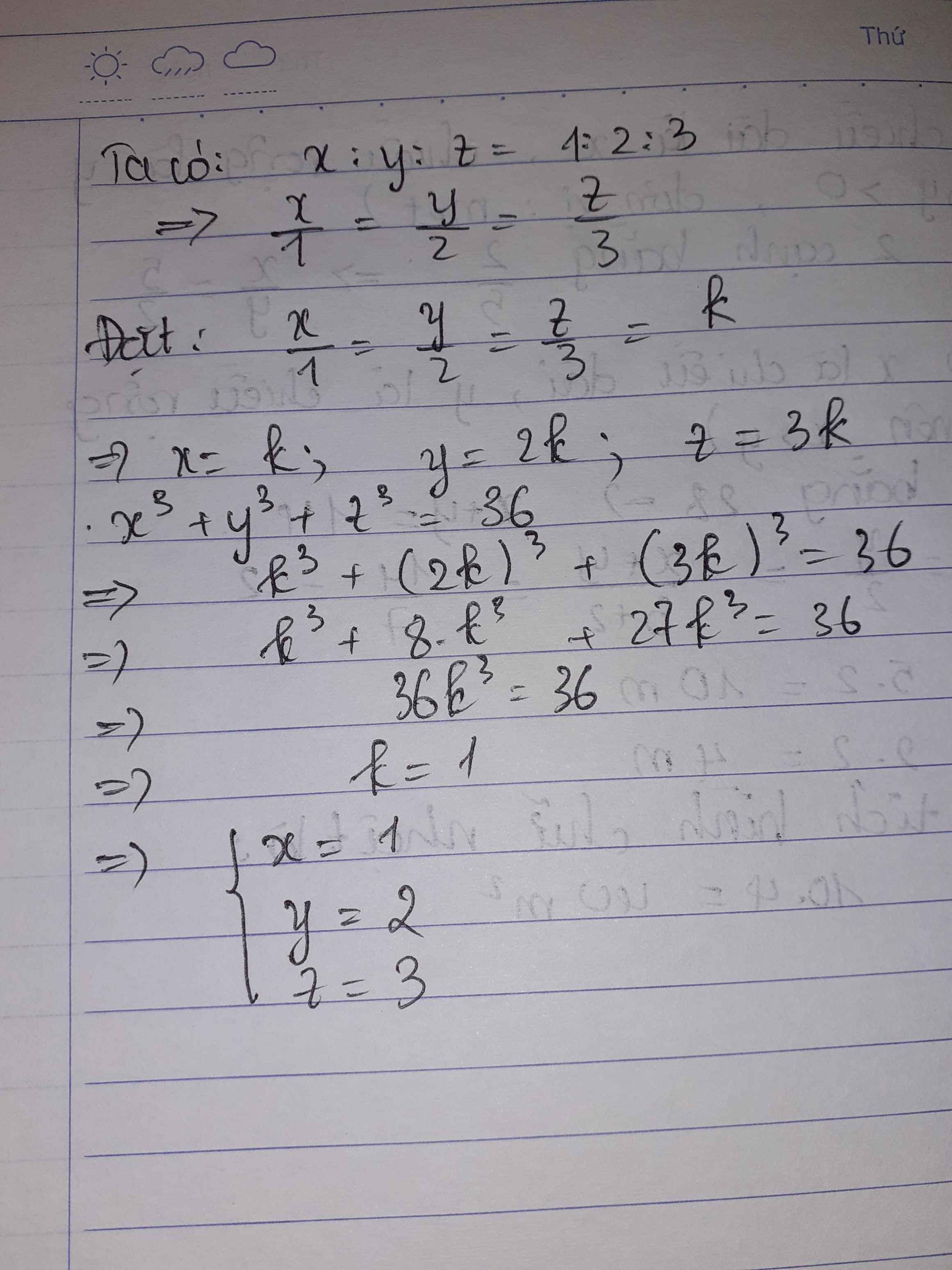
\(-3x\left(x+2\right)^2+\left(x+3\right)\left(x-1\right)\left(x+1\right)-\left(2x-3\right)^2\)
\(=-3x\left(x^2+4x+4\right)+\left(x+3\right)\left(x^2-1\right)-\left(4x^2-12x+9\right)\)
\(=-3x^3-12x^2-12x+x^3-x+3x^2-3-4x^2+12x-9\)
\(=-2x^3-13x^2-x-12\)
8 tháng 1 2019
a,A=|x-7|+12
Vì \(\left|x-7\right|\ge0\forall x\)nên \(\left|x-7\right|+12\ge12\forall x\)
Ta thấy A=12 khi |x-7| = 0 => x-7 = 0 => x = 7
Vậy GTNN của A là 12 khi x = 7
b,B=|x+12|+|y-1|+4
Vì \(\left|x+12\right|\ge0\forall x\)
\(\left|y-1\right|\ge0\forall y\)
nên \(\left|x+12\right|+\left|y-1\right|\ge0\forall x,y\)
\(\Rightarrow\left|x+12\right|+\left|y-1\right|+4\ge4\forall x,y\)
Ta thấy B = 4 khi \(\hept{\begin{cases}\left|x+12\right|=0\\\left|y-1\right|=0\end{cases}}\Rightarrow\hept{\begin{cases}x+12=0\\y-1=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-12\\y=1\end{cases}}\)
Vậy GTNN của B là 4 khi x = -12 và y = 1
TA
21 tháng 7 2021
Các cạnh `x,y,z` tỉ lệ với `2,4,5 => x:y:z=2:4:5 <=> x/2=y/4=z/5`
Tổng độ dài của cạnh lớn nhất và nhỏ nhất hơn cạnh còn lại `20cm`
`=> z+x=y+20<=>x-y+z=20`
Áp dụng tính chất của dãy tỉ số bằng nhau:
`x/2=y/4=z/6=(x-y+z)/(2-4+6)=20/4=5`
`=>x=2.5=10`
`y=4.5=20`
`z=5.5=25`
Vậy...
21 tháng 7 2021
Gọi 33 cạnh của tam giác đó lần lượt là x;y;z(cm,0<x<y<z)x;y;z(cm,0<x<y<z).
Theo bài ra ta có: x/2=y/4=z/5 và x+z−y=20
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
x/2=y/4=z/5=x+z−y/2+5−4=20/3
x/2=20/3⇒x=403(tm)
y/4=20/3⇒y=80/3(tm)
z/5=20/3⇒z=100/3(tm)
Vậy độ dài 33 cạnh của tam giác đó lần lượt là: 403cm;803cm;1003cm403cm;803cm;1003cm.
tick cho mình nha!
NC
10 tháng 8 2020
Bài làm:
a) Ta có: \(\left(-\frac{3}{8}x^2z\right).\left(\frac{2}{3}xy^2z^2\right).\left(\frac{4}{5}x^3y\right)\)
\(=-\frac{1}{5}x^6y^3z^3\)
b) Tại x=-1 ; y=-2 ; z=3 thì giá trị đơn thức là:
\(-\frac{1}{5}.\left(-1\right)^6.\left(-2\right)^3.3^3=\frac{216}{5}\)
10 tháng 8 2020
a) Ta có : \(\left(\frac{-3}{8}x^2z\right)\cdot\frac{2}{3}xy^2z^2\cdot\frac{4}{5}x^3y=\left(-\frac{3}{8}\cdot\frac{2}{3}\cdot\frac{4}{5}\right)\cdot x^2xx^3\cdot y^2y\cdot zz^2=-\frac{1}{5}x^6y^3z^3\)
b) Với x = -1 ; y = -2 , z = 3
Thế vào ba đơn thức trên và đơn thức tích ta được :
\(\frac{-3}{8}x^2z=\frac{-3}{8}\left(-1\right)^2\cdot3=\frac{-3}{8}\cdot1\cdot3=\frac{-9}{8}\)
\(\frac{2}{3}xy^2z^2=\frac{2}{3}\cdot\left(-1\right)\cdot\left(-2\right)^2\cdot3^2=\frac{2}{3}\left(-1\right)\cdot4\cdot9=-24\)
\(\frac{4}{5}x^3y=\frac{4}{5}\left(-1\right)^3\cdot\left(-2\right)=\frac{4}{5}\left(-1\right)\left(-2\right)=\frac{8}{5}\)
\(-\frac{1}{5}x^6y^3z^3=-\frac{1}{5}\left(-1\right)^6\left(-2\right)^3\cdot3^3=-\frac{1}{5}\cdot1\cdot\left(-8\right)\cdot27=\frac{216}{5}\)
XO
1 tháng 8 2021
Ta có \(5x=3y\Rightarrow\frac{x}{3}=\frac{y}{5}\)
Áp dụng dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{5}=\frac{x-y}{3-5}=\frac{10}{-2}=-5\)
\(\Rightarrow x=3.\left(-5\right)=-15;y=\left(-5\right).5=-25\)
Vậy x = -15 ; y = -25
9 tháng 3 2020
A)\(\left|x+1\right|+\left|x+1\right|=2\)
\(\Rightarrow2.\left|x+1\right|=2\)
\(\Rightarrow\left|x+1\right|=2:2\)
\(\Rightarrow\left|x+1\right|=1\)
\(\Rightarrow x+1=1\) hoặc \(x+1=-1\)
1)x+1=1 2)x+1=-1
\(\Rightarrow x=1-1\) \(\Rightarrow x=-1-1\)
\(\Rightarrow x=0\) \(\Rightarrow x=-2\)
Vậy \(x\in\left\{0;-2\right\}\)
b) x-[-x+(x+3)]-[(x+3)-(x-2)]=0
\(\Rightarrow x-\left[-x+x+3\right]-\left[x+3-x+2\right]=0\)
\(\Rightarrow x-3-5=0\)
\(\Rightarrow x=0+3+5\)
\(\Rightarrow x=8\)
Vậy x=8
c)\(\left(3x+1\right)^2+\left|y-5\right|=1\)
+)Giả sử 3x+1 là số âm
\(\Rightarrow\left(3x+1\right)^2\)là số dương(1)
+)Lại giả sử 3x+1 là số dương
\(\Rightarrow\left(3x+1\right)^2\)là số dương(2)
+)Từ (1) và (2)
\(\Rightarrow\left(3x+1\right)^2\)nguyên dương với mọi x
+)Ta có:\(\left(3x+1\right)^2\ge0;\left|y-5\right|\ge0\)
\(\Rightarrow\left(3x+1\right)^2=1;\left|y-5\right|=0\)
\(\Rightarrow x=0;y=5\)
+)Ta lại có:\(\left(3x+1\right)^2\ge0;\left|y-5\right|\ge0\)
\(\Rightarrow\left(3x+1\right)^2=0;\left|y-5\right|=1\)
\(\Rightarrow x=\frac{-1}{3};y\in\left\{6;4\right\}\)
Mà \(\left(x,y\right)\in Z\)
\(\Rightarrow x=0;y=5\)
Đề bạn thiếu x,y thuộc Z đó
Chúc bn học tốt
TT
23 tháng 2 2020
Ta thấy : \(\frac{1}{11}>\frac{1}{100},\frac{1}{12}>\frac{1}{100},...,\frac{1}{100}=\frac{1}{100}\)
\(\Rightarrow\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+...+\frac{1}{100}>\frac{1}{100}+\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}=\frac{90}{100}=\frac{9}{10}\)
\(\Rightarrow\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+...+\frac{1}{100}>\frac{9}{10}+\frac{1}{10}=1\)
Do đó : \(\frac{1}{10}+\frac{1}{11}+\frac{1}{12}+\frac{1}{13}+...+\frac{1}{100}>1\)