Giúp mình giải bài bài này với😥😥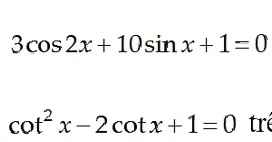
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


`sin(2x-π/3)+1=0`
`<=>sin(2x-π/3)=-1`
`<=>2x-π/3=-π/2=k2π`
`<=>x=(5π)/12+kπ (k \in ZZ)`
Có: `-2020π < (5π)/12+kπ < 2020π`
`<=> -2020 < 5/12+k<2020`
`<=>-2020-5/12 <k<2020+5/12`
`=> k \in {-2020;.....;2020}`
`=>` Có `4041` giá trị của `k` thỏa mãn.


Gọi \(M\left(x;y\right)\) là 1 điểm bất kì trên (E) \(\Rightarrow\dfrac{x^2}{16}+\dfrac{y^2}{9}=1\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép tịnh tiến \(\overrightarrow{v}\Rightarrow M'\in\left(E'\right)\) với (E') là ảnh của (E) qua phép tịnh tiến nói trên
\(\left\{{}\begin{matrix}x'=x+3\\y'=y-2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'-3\\y=y'+2\end{matrix}\right.\)
Thế vào (1):
\(\dfrac{\left(x'-3\right)^2}{16}+\dfrac{\left(y'+2\right)^2}{9}=1\)
Hay pt (E') có dạng: \(\dfrac{\left(x-3\right)^2}{16}+\dfrac{\left(y+2\right)^2}{9}=1\)


PTHH: \(2NaOH+H_2SO_4\rightarrow Na_2SO_4+2H_2O\)
Ta có: \(n_{H_2SO_4\left(dư\right)}=\dfrac{1}{2}n_{NaOH}=\dfrac{0,1\cdot1}{2}=0,05\left(mol\right)\)
\(\Rightarrow n_{H_2SO_4\left(p.ứ\right)}=0,3\cdot2-0,05=0,55\left(mol\right)\)
PTHH: \(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
a________\(\dfrac{3}{2}\)a (mol)
\(Fe+H_2SO_4\rightarrow FeSO_4+H_2\)
b_______b (mol)
Ta lập hệ phương trình: \(\left\{{}\begin{matrix}27a+56b=16,6\\\dfrac{3}{2}a+b=0,55\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{71}{285}\\b=\dfrac{67}{380}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\%m_{Al}=\dfrac{\dfrac{71}{285}\cdot27}{16,6}\cdot100\%\approx40,52\%\\\%m_{Fe}=59,48\%\end{matrix}\right.\)







3cos2x + 10sinx + 1 = 3( 1 - 2sinx^2) + 10 sinx + 1
= - 6 sinx^2 + 10sinx + 4
= 2(3sinx + 1)(2- sinx)= 0
ý 2 là trên đoạn nào bn ?