Cho đa thức bậc 2 , 1 biến có dạng ax2 + bx + c ( a , b , c thuộc Z ) . Chứng minh rằng đa thức đó sẽ không phân tích thành nhân tử được nữa nếu b2 - 4ac > 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 8 2017
* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
CM
29 tháng 11 2018
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
CM
4 tháng 6 2017
* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: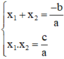 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
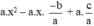
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm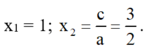 
Vậy: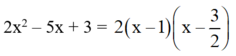 
LM
3
HP
14 tháng 8 2016
\(\left(x+a\right)\left(x+b\right)\left(x+c\right)=\left(x^2+bx+ax+ab\right)\left(x+c\right)\)
\(=x^3+cx^2+bx^2+bcx+ax^2+acx+abx+abc\)
\(=x^3+\left(a+b+c\right)x^2+\left(ab+ac+bc\right)x+abc\)
Đồnh nhất đa thức trên với đa thức \(x^3+ax^2+bx+c\),ta đc hệ điều kiện:
\(\hept{\begin{cases}a+b+c=a\left(1\right)\\ab+ac+bc=b\left(2\right)\\abc=c\left(3\right)\end{cases}}\)
Từ \(\left(1\right)a+b+c=a=>b+c=0=>c=-b\)
Thay vào (2),ta đc: \(ab+a.\left(-b\right)+b.\left(-b\right)=b=>ab-ab-b^2=b=>-b^2=b\)
\(=>b^2+b=0=>b\left(b+1\right)=0=>\orbr{\begin{cases}b=0\\b=-1\end{cases}}\)
+b=0 thì từ (1) suy ra c=0 ; a tùy ý
+b=-1 thì từ (1) suy ra c=1
Mà theo (3)\(abc=c=>a=\frac{c}{bc}=\frac{1}{-1}=-1\)
Vậy a=-1 hoặc a tùy ý ;b=0 hoặc b=-1;c=0 hoặc c=1
9 tháng 5 2023
a: f(1)=a+b+c=0
=>x=1 là nghiệm
b: Vì 5-6+1=0
nên f(x)=5x^2-6x+1 có một nghiệm là x=1
Sai rồi, là b2 - 4ac < 0 mà thớt.