Bài 3. Cho tam giác đều ABC. Gọi D, E lần lượt là trung điểm của các cạnh AB và
AC.
a) Chứng minh: BDEC là hình thang cân có đáy nhỏ bằng cạnh bên.
b) Tính chu vi hình thang cân BDEC biết AB = 6cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
25 tháng 6 2021
a) Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(AB=AC;AD=AE\right)\)
D\(\in\)AB(gt)
E\(\in\)AC(gt)
Do đó: DE//BC(Định lí Ta lét đảo)
Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang(Định nghĩa hình thang)
Hình thang BDEC(DE//BC) có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
CM
14 tháng 12 2017
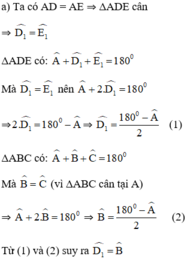
Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
7 tháng 11 2021
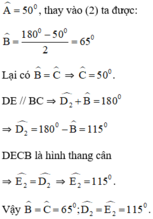
b: Xét ΔABC có
F là trung điểm của AB
E là trung điểm của AC
Do đó: FE là đường trung bình của ΔABC
Suy ra: FE//BD và FE=BD
hay BDEF là hình bình hành
27 tháng 8 2021
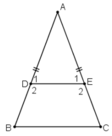
a, Vì AD = AE nên \(\Rightarrow\Delta ADE\)là tam giác cân tại A
\(\Rightarrow gócADE\)\(=\frac{180^o-A}{2}\)
Vì \(\Delta ABC\)cân tại A nên
Góc CBA = \(\frac{180^o-A}{2}\)
\(\Rightarrow ADE=CBA\)( mà 2 góc này nằm trong vị trí so le trong )
\(\Rightarrow\)\(DE//BC\)
Mà \(ABC=ACB\)(Vì tam giác ABC cân tại A )
\(\Rightarrow\)Tứ giác BDEC là hình thang cân
b,
Ta có :
^A \(=70^o\)\(\Rightarrow\)^B=^C =\(55^O\)
\(\Rightarrow BDE=CED=\frac{\left(360-2\cdot55\right)}{2}=125^O\)
14 tháng 8 2021
Xét ΔABC có
BE là đường phân giác ứng với cạnh AC
nên \(\dfrac{AE}{EC}=\dfrac{AB}{BC}\left(1\right)\)
Xét ΔABC có
CD là đường phân giác ứng với cạnh AB
nên \(\dfrac{AD}{DB}=\dfrac{AC}{BC}\left(2\right)\)
Ta có: ΔBAC cân tại A
nên \(AB=AC\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra \(\dfrac{AD}{DB}=\dfrac{AE}{EC}\)
hay DE//BC
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà \(\widehat{DBC}=\widehat{ECB}\)
nên BDEC là hình thang cân
Xét ΔEDC có \(\widehat{EDC}=\widehat{ECD}\left(=\widehat{DCB}\right)\)
nên ΔEDC cân tại E
Suy ra: ED=EC=BD
a) Xét ΔABC có
D là trung điểm của AB(gt)
E là trung điểm của AC(gt)
Do đó: DE là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)
Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang có hai đáy là DE và BC(Định nghĩa hình thang)
Hình thang BDEC(BC//DE) có \(\widehat{B}=\widehat{C}\left(=60^0\right)\)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Ta có: \(DE=\dfrac{BC}{2}\)(cmt)
\(BD=\dfrac{1}{2}AB\)(D là trung điểm của AB)
\(EC=\dfrac{1}{2}AC\)(E là trung điểm của AC)
mà BC=AB=AC(ΔABC đều)
nên DE=BD=EC
Vậy: BDEC là hình thang cân có đáy nhỏ bằng cạnh bên
b) Ta có: \(DE=BD=EC=\dfrac{AB}{2}\)(cmt)
nên DE=BC=EC=3(cm)
Chu vi hình thang BDEC là:
C=DE+DB+EC+BC=3+3+3+6=15(cm)