Em đang cần gấp bài này mng giải hộ em với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DL
0
TP
20 tháng 8 2021
1/ \(n_S=\dfrac{6,4}{32}=0,2;n_{H_2SO_4}=\dfrac{14.70\%}{98}=0,1\)
Bảo toàn nguyên tố S : \(n_S=n_{H_2SO_4\left(lt\right)}=0,2\)
Mà thực tế chỉ thu được 0,1
=> \(H=\dfrac{0,1}{0,2}.100=50\%\)
TP
20 tháng 8 2021
2/ \(n_{N_2}=0,2\left(mol\right);n_{H_2}=0,3\left(mol\right);n_{NH_3}=0,15\left(mol\right)\)
PTHH: \(N_2+3H_2\rightarrow2NH_3\)
Lập tỉ lệ : \(\dfrac{0,2}{1}>\dfrac{0,3}{3}\)=> Sau phản ứng N2 dư, tính theo số mol H2
=> n NH3(lt)= \(\dfrac{0,3.2}{3}=0,2\left(mol\right)\)
Mà thực tế chỉ thu được 0,15 mol
=> \(H=\dfrac{0,15}{0,2}.100=75\%\)
MA
1
23 tháng 11 2021
a) \(P=U.I\Rightarrow I=\dfrac{P}{U}=\dfrac{75}{220}=\dfrac{15}{44}\left(A\right)\)
b) \(A=P.t=75.30.4.60.60=32400000\left(J\right)=9\left(kWh\right)\)
c) Tiền điện phải trả: \(9.2000=18000\left(đồng\right)\)
HK
1
A
1
12 tháng 12 2021
a: Xét tứ giác OBAC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
Do đó: OBAC là tứ giác nội tiếp
NA
0
8 tháng 9 2021
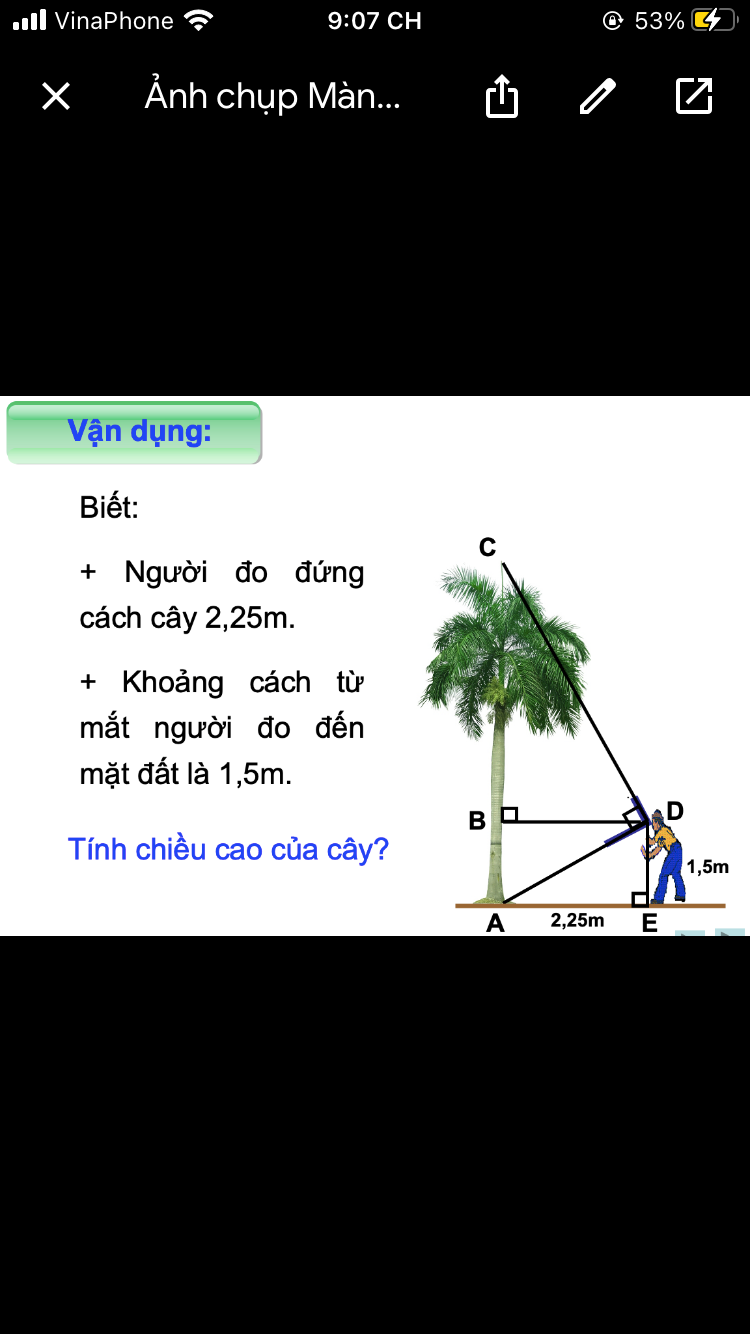
Xét tam giác ADE vuông tại E có:
\(AD^2=AE^2+DE^2\)(định lý Pytago)
\(\Rightarrow AD^2=\dfrac{117}{16}\left(m\right)\)
Xét tam giác ADC vuông tại D có đường cao DB có:
\(AD^2=AB.AC\)(hệ thức lượng trong tam giác vuông)
\(\Rightarrow AC=\dfrac{AD^2}{AB}=\dfrac{117}{16}:1,5=\dfrac{39}{8}\left(m\right)\)
Vậy chiều cao của cây là \(\dfrac{39}{8}m\)
mọi người giải giúp em bài này với ạ em đang cần gấp ạ
26 tháng 9 2021
a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)
1) \(A=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}:\dfrac{\sqrt{x}-1}{5}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{5}{\sqrt{x}-1}\) \(=\dfrac{5}{x+\sqrt{x}+1}\)
2) Ta thấy \(x+\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}+1\right)+1>1\forall x\)
\(\Rightarrow A< 5\)