Giải hộ e câu này theo cách lớp 8 ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Gọi \(x\left(x\in N\right)\) là số học sinh lớp 8A
Theo đề bài, ta có pt :
\(\left(\dfrac{3}{8}x+4\right)=50\%x\)
\(\Leftrightarrow\left(\dfrac{3}{8}x+4\right)=\dfrac{1}{2}x\)
\(\Leftrightarrow\dfrac{3}{8}x-\dfrac{1}{2}x=-4\)
\(\Leftrightarrow-\dfrac{1}{8}x=-4\)
\(\Leftrightarrow x=32\left(tmdk\right)\)
Vậy lớp 8A có 32 học sinh




Câu 8 :B
m NaCl = 200.5% = 10(gam)
m H2O = m dd - m NaCl = 200 - 10 = 190(gam)
Câu 8:
mNaCl=5%.200=10(g)
=>mH2O=mddNaCl - mNaCl= 200-10=190(g)
=> Điều chế: Hòa tan 10 gam NaCl vào 190 gam H2O
=> CHỌN B

a: ΔAMN vuông tại A
mà AI là đường trung tuyến
nên AI=IM=IN=MN/2
=>I là tâm đường tròn ngoại tiếp ΔAMN
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: Xét ΔABC vuông tại A có AM là đường cao
nên \(\left\{{}\begin{matrix}AB\cdot AC=AM\cdot BC\\AB^2=BM\cdot BC\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}AM=\dfrac{12\cdot16}{20}=9.6\left(cm\right)\\BM=\dfrac{12^2}{20}=7.2\left(cm\right)\end{matrix}\right.\)
c: ΔABM vuông tại M có ME là đường cao
nên \(AE\cdot AB=AM^2\)
ΔAMC vuông tại M
=>\(MA^2+MC^2=AC^2\)
=>\(MA^2=AC^2-MC^2\)
=>\(AE\cdot AB=AC^2-MC^2\)






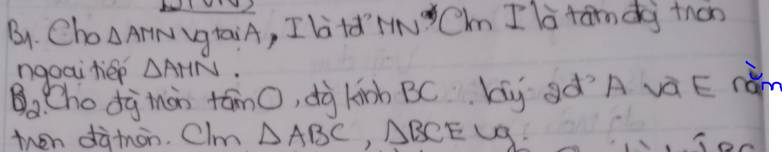
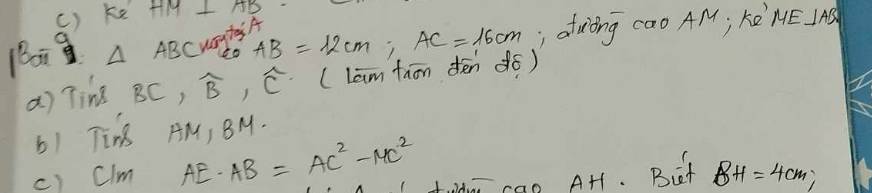
\(n_{Fe}=\dfrac{11.2}{56}=0.2\left(mol\right)\)
\(Fe+2HCl\rightarrow FeCl_2+H_2\left(1\right)\)
\(0.2................................0.2\)
\(2Al+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\left(2\right)\)
\(a.................................1.5a\)
Vì : cân thăng bằng nên :
\(m_{Fe}-m_{H_2\left(1\right)}=m_{Al}-m_{H_2\left(2\right)}\)
\(\Leftrightarrow11.2-0.2\cdot2=27a-1.5\cdot2a\)
\(\Leftrightarrow a=0.45\)
\(m_{Al}=0.45\cdot27=12.15\left(g\right)\)