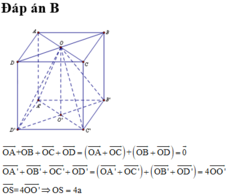
Cho hình vuông ABCD tâm O. Tính độ dài |2AB+3OC| (vector hay còn gọi là véc tơ ạ).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường và AC=BD
=>O là trung điểm chung của AC và BD
ABCD là hình chữ nhật
=>AB=CD=2a; BC=AD
O là trung điểm của AC
=>\(AC=2\cdot AO=2a\cdot\sqrt{5}\)
=>\(BD=2a\sqrt{5}\)
ABCD là hình chữ nhật
=>ΔABC vuông tại B
=>\(BA^2+BC^2=AC^2\)
=>\(BC^2=AC^2-AB^2=\left(2a\sqrt{5}\right)^2-\left(2a\right)^2=20a^2-4a^2=16a^2\)
=>BC=4a
=>\(\left|\overrightarrow{BC}\right|=4a\)

1) Các vecto bằng vecto EF là:
\(\overrightarrow{EF}=\overrightarrow{DO}=\overrightarrow{OA}=\overrightarrow{CB}\)

Chọn đáp án C
Do O là tâm đường tròn nội tiếp hình vuông ABCD nên bán kính đường tròn nội tiếp hình vuông là:
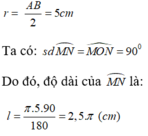

Xét B thuộc đường tròn (O), B' đối xứng với B qua O => BB' là đường kính của (O)
=> AB' vuông góc AB. Mà CH vuông góc AB nên AB' // CH. Tương tự AH // B'C
Suy ra tứ giác AHCB' là hình bình hành => AH // B'C và AH = B'C => \(\overrightarrow{AH}=\overrightarrow{B'C}\)(đpcm).