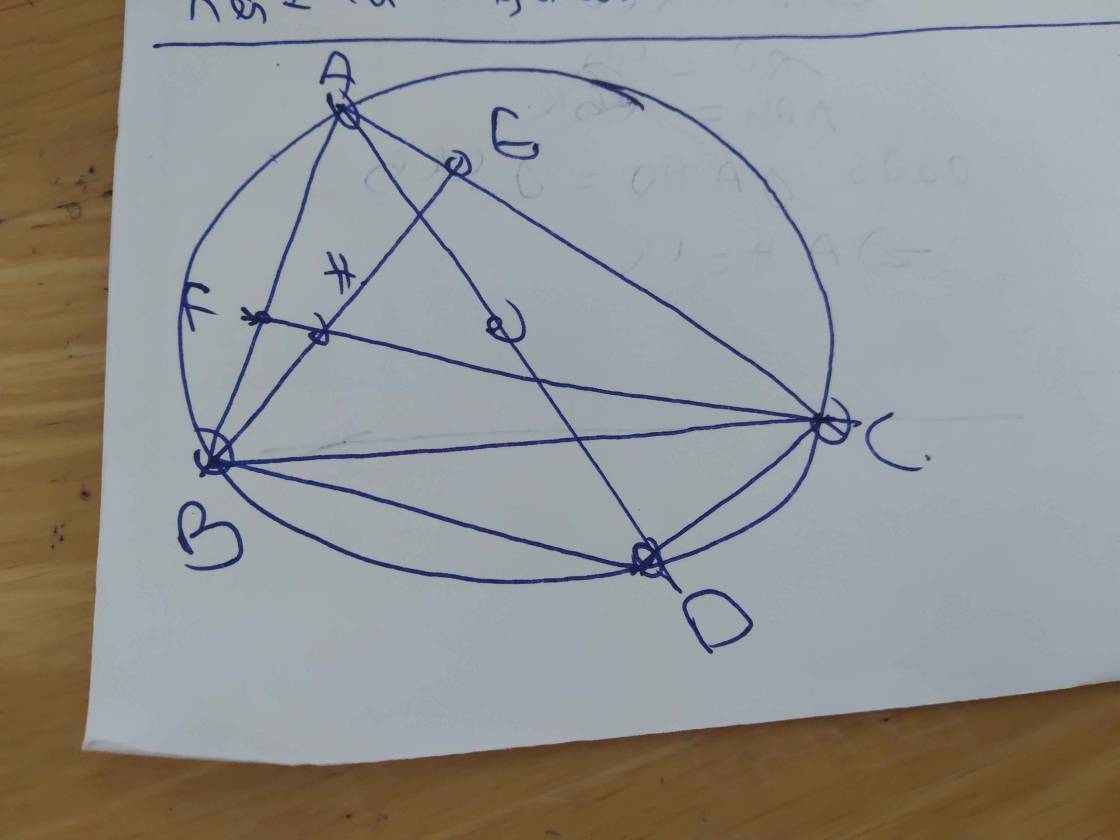
1. Cho tam giác ABC nội tiếp đương tròn O. Đường cao AD cắt đường tròn tại E, vẽ đường kính AM.
a. Chứng minh rằng: BEMC là hình thang cân
b. Chứng minh rằng: DA2 + DB2 + DE2 + DC2 = 4.R2
2. Cho tam giác ABC đều, đường cao AH, điểm M thuộc BC. Gọi P và Q là hình chiếu của M trên AB, AC.
a. Chứng minh rằng: A, P, M, H, Q thuộc 1 đường tròn. Xác định tâm O của đường tròn đó.
b. Chứng minh rằng: OM vuông góc PQ.
c. Chứng minh rằng: MP+MQ=AH
d. Xác định vị trí điểm M sao cho độ dài PQ nhỏ nhất.
Giúp mình với. Cảm ơn ạ!