Cho tam giác ABC, hai đường phân giác BE và CF cắt nhau tại I.
a) Chứng minh: Nếu S đối xứng với E qua CF cũng là điểm đối xứng của F qua BE thì tam giác EFS đều.
b) Suy ra rằng góc A = 60 độ.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

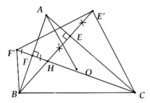
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi

b: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
=>BHCD là hình bình hành
=>BH//CD và BD//CH
ta có: BH//CD
BH\(\perp\)AC
Do đó: CD\(\perp\)CA
=>ΔCDA vuông tại C
=>ΔCAD nội tiếp đường tròn đường kính AD(1)
Ta có: BD//CH
CH\(\perp\)AB
Do đó: BD\(\perp\)BA
=>ΔBAD vuông tại B
=>ΔBAD nội tiếp đường tròn đường kính AD(2)
Từ (1) và (2) suy ra B,A,D,C cùng thuộc (O), đường kính AD
Xét (O) có
ΔAID nội tiếp
AD là đường kính
Do đó: ΔAID vuông tại I
=>AI\(\perp\)ID tại I
=>AI\(\perp\)IH tại I
=>ΔAIH vuông tại I
=>I nằm trên đường tròn đường kính AH(3)
ta có: \(\widehat{AFH}=\widehat{AEH}=90^0\)
=>A,F,H,E cùng thuộc đường tròn đường kính AH(4)
Từ (3) và (4) suy ra A,F,I,H,E cùng thuộc một đường tròn
cho l-i-k-e đi mình giải cho , mình biết rùi