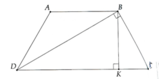
hình thang cân ABCD ( AB //CD ) có DB là tia phân giác của góc D , DB vuông góc BC. Biết AB = 10 cm, CD=24 cm . tính chu vi hình thang
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 9 2021
\(\widehat{ABD}=\widehat{BDC}\left(SLT\right);\widehat{ADB}=\widehat{BDC}\left(GT\right)\\ \Rightarrow\widehat{ABD}=\widehat{ADB}\Rightarrow AD=AB=BC=4\left(cm\right)\)
(tam giác \(ADB\) cân tại \(A\))
Vì là h.thang cân mà có: BD là phân giác \(\widehat{D}\) nên AC cũng là phân giác \(\widehat{C}\) \(\Rightarrow\widehat{ACB}=\widehat{ACD}\)
Dễ thấy các góc bằng nhau: \(\widehat{BAC}=\widehat{ADB}=\widehat{BDC}=\widehat{ACD}=\widehat{ACB}=\widehat{ABD};\widehat{DBC}=\widehat{DAC}=90\)
\(\Rightarrow6\widehat{BDC}+90+90=360\Rightarrow\widehat{BDC}=30\)
\(\sin\widehat{BDC}=\dfrac{BC}{DC}\Rightarrow DC=\dfrac{BC}{\sin\widehat{BDC}}=\dfrac{4}{\sin30}=8\left(cm\right)\)
\(\Rightarrow P_{ABCD}=4+4+8+4=20\left(cm\right)\)
T
5 tháng 9 2021
Vì AB // DC => góc ABD = góc BDC
Mà góc ADB = góc BDC ( DB là phân giác ADC )
=> góc ABD = góc ADB
=> tam giác ADB cân tại A
=> AD = AB = 4 (cm)
Mà ABCD là hình thang cân
=> AD = BC = 4 (cm)
Có : góc BDC = 1/2 góc ADC
mà góc ADC = góc BCD ( ABCD là hình thang cân )
=> góc BDC = 1/2 góc BCD => góc BCD = 2 . BDC
Xét tam giác BCD vuông tại B có
BDC + BCD = 90
<=> BDC + 2BDC = 90
<=> BDC = 30
mà BC là cạnh đối diện góc BDC
=> BC = 1/2 BD
Hay 4 = 1/2 BD
=> BD = 8 (cm)
Áp dụng ĐL Pytago vào tam giác BDC vuông tại B được
BC2 + DC2 = BD2
<=> DC = \(\sqrt{BD^2-BC^2}\)
<=> DC= \(\sqrt{8^2-4^2}=4\sqrt{3}\)
Vậy chu vi hình thang ABCD là
AB + BC + CD + AD = 4 + 4 + 4\(\sqrt{3}\) + 4 =12 + 4\(\sqrt{3}\) ( cm )
10 tháng 7 2017
)Theo đề bài ABCD là ht cân đáy AB//CD
=>AD=BC=3cm (cạnh bên htc với BC=3cm-gt)
Kẻ BE//AD (E thuộc CD) thì
tứ giác ABED là hbh (2 cặp cạnnh //).Hình bh đó có đ/chéo DB cũng là phân giác góc D (gt) nên hbh ABED là h/thoi
=>DE=AB=BE=AD=3cm và AE vuông góc BD (tính chất 2 đ/chéo h/thoi)
Vậy AE//BC (cùng vuông góc với BD)
nên tứ giác ABCE cũng là hbh (2 cặp cạnh //).Hình bh đó có AB=BC nên hbh ABCE là h/thoi
=> CE=CB=3cm
Mặt khác tam giác BCE có BC=CE=EB=3cm nên tam giác BCE là tam giác đều
=> góc CBE=60o < góc CBD=1v (gt)
=> tia BE nằm giữa 2 tia BC,BD
=> điểm E nằm giữa 2 điểm C,D
=> CD= CE+ED=3cm+3cm
Vậy chu vi htc ABCD=5.3cm=15cm
14 tháng 7 2017
)Theo đề bài ABCD là ht cân đáy AB//CD
=>AD=BC=3cm (cạnh bên htc với BC=3cm-gt)
Kẻ BE//AD (E thuộc CD) thì
tứ giác ABED là hbh (2 cặp cạnnh //).Hình bh đó có đ/chéo DB cũng là phân giác góc D (gt) nên hbh ABED là h/thoi
=>DE=AB=BE=AD=3cm và AE vuông góc BD (tính chất 2 đ/chéo h/thoi)
Vậy AE//BC (cùng vuông góc với BD)
nên tứ giác ABCE cũng là hbh (2 cặp cạnh //).Hình bh đó có AB=BC nên hbh ABCE là h/thoi
=> CE=CB=3cm
Mặt khác tam giác BCE có BC=CE=EB=3cm nên tam giác BCE là tam giác đều
=> góc CBE=60o < góc CBD=1v (gt)
=> tia BE nằm giữa 2 tia BC,BD
=> điểm E nằm giữa 2 điểm C,D
=> CD= CE+ED=3cm+3cm
Vậy chu vi htc ABCD=5.3cm=15cm
CM
10 tháng 1 2018
a) DDBC vuông có B C D ^ = 2 B D C ^ nên A D C ^ = B C D ^ = 60 0 và D A B ^ = C B A ^ = 120 0
b) Tính được DC = 2.BC = 12cm, suy ra PABCD = 30cm.
Hạ đường cao BK, ta có BK = 3 3 c m .
Vậy SABCD = 27 3 c m 2
