Cho By//Ax với Ax, By cùng phía với AB. Gọi C là một điểm bát kì trên mặt phẳng biết góc Cax bằng 300 và góc CBy bằng 400. Tính góc ACB.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án C
Phương pháp: Δ φ = 2 π d λ
Cách giải:
+ Áp dụng hệ thức lượng trong tam giác vuông OMN có đường cao OH:
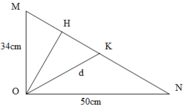
1 O H 2 = 1 O M 2 + 1 O N 2 ⇔ 1 O H 2 = 1 34 2 + 1 50 2 ⇒ O H = 28,1 c m
+ Gọi d là khoảng cách từ O đến K (K là 1 điểm bất kì trên MN)
+ Độ lệch pha giữa K và O là: Δ φ = 2 π d λ
+ Để K dao động cùng pha với O thì: Δ φ = 2 π d λ = 2 k π ⇒ d = k λ
+ Số điểm dao động cùng pha với o trên đoạn MN bằng số giá trị k nguyên thoả mãn:
28,1 ≤ k λ ≤ 34 ⇒ 7,025 ≤ k ≤ 8,5 ⇒ k = 8 28,1 < k λ ≤ 50 ⇒ 7,025 < k ≤ 12,5 ⇒ k = 8 ; 9 ; 10 ; 11 ; 12
Có 6 giá trị của k thoả mãn ⇒ trên đoạn MN có 6 điểm dao động cùng pha với nguồn

5:
a: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
b: Xét ΔAEB vuông tại E và ΔDAB vuông tại A có
góc ABE chung
=>ΔAEB đồng dạng với ΔDAB
c: ΔABD vuông tại A có AE là đường cao
nên BE*BD=BA^2
ΔABC vuông tại A có AH là đường cao
nên BH*BC=BA^2
=>BE*BD=BH*BC
d: BE*BD=BH*BC
=>BE/BC=BH/BD
=>ΔBEH đồng dạng với ΔBCD
=>góc BHE=góc BDC

Trả lời hộ mình cái xin. mình đã 2 năm ko on r giờ mới on lại :(((.Xin mọi người trả lời giúp mình :(((


bạn tự vẽ hình
vì Ax // By nên góc xAB + góc yBA = 180 độ (hai góc trong cùng phía thì bù nhau, tính chất song song)
=> góc CAB + góc CBA = 180 -( 30 + 40 ) = 110
mà tổng 3 góc của 1 tam giác = 180 nên góc ACB = 70 độ