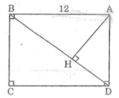
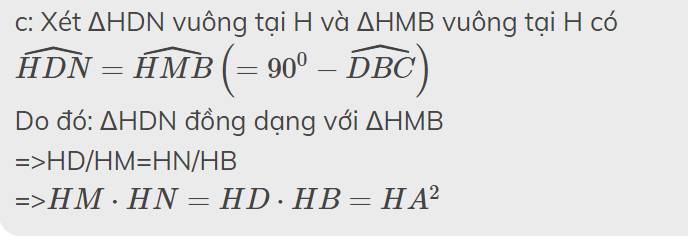cho hình chữ nhật ABCD, AB=9cm, BC=12cm. kẻ CK vuông góc với BD. tính diện tích AKD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 5 2022
Áp dụng định lý pitago: \(AC=\sqrt{12^2+9^2}=\sqrt{225}=15\left(cm\right)\)
Xét tam giác HBA và tam giác ABC, có:
\(\widehat{BHA}=\widehat{ABC}=90^o\)
\(\widehat{A}\): chung
Vậy tam giác HAB đồng dạng tam giác BAC ( g.g )
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AB}{AC}=\dfrac{HB}{BC}\)
\(\Rightarrow AH=\dfrac{AB^2}{AC}=\dfrac{12^2}{15}=9,6\left(cm\right)\)
\(\Rightarrow HB=\dfrac{AB.BC}{AC}=\dfrac{12.9}{15}=7,2\left(cm\right)\)
\(S_{AHB}=\dfrac{1}{2}.AH.HB=\dfrac{1}{2}.9,6.7,2=34,56\left(cm^2\right)\)
29 tháng 5 2022
a,
Xét Δ HBA và Δ BAC, có :
\(\widehat{BHA}=\widehat{ABC}=90^o\)
\(\widehat{ABH}=\widehat{CAB}\) (cùng phụ \(\widehat{ABC}\))
=> Δ HBA ~ Δ BAC (g.g)
31 tháng 10 2023
a: ΔABD vuông tại A
=>\(BD^2=AB^2+AD^2\)
=>\(BD^2=9^2+12^2=225\)
=>BD=15(cm)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH\cdot BD=AB\cdot AD\)
=>\(AH\cdot15=12\cdot9=108\)
=>AH=108/15=7,2(cm)
XétΔABD vuông tại A có \(sinBDA=\dfrac{AB}{BD}=\dfrac{9}{15}=\dfrac{3}{5}\)
nên \(\widehat{BDA}\simeq37^0\)
b: Xét ΔAHB vuông tại H có HI là đường cao
nên \(AI\cdot AB=AH^2\left(1\right)\)
Xét ΔABD vuông tại A có AH là đường cao
nên \(AH^2=HD\cdot HB\left(2\right)\)
Từ (1) và (2) suy ra \(AI\cdot AB=HD\cdot HB\)
c: Xét ΔHDN vuông tại H và ΔHMB vuông tại H có
\(\widehat{HDN}=\widehat{HMB}\left(=90^0-\widehat{DBC}\right)\)
Do đó: ΔHDN đồng dạng với ΔHMB
=>HD/HM=HN/HB
=>\(HM\cdot HN=HD\cdot HB=HA^2\)
LC
3 tháng 4 2018
a)
vì ABCD hình chữ nhật nên ta có AB//CD
=> góc ABH= góc BDC ( so le trong, AB//CD)
xét tam giác AHB,BCD có
góc A= góc C =90
góc ABH=BDC(cmt)
=> tam giác AHB đồng dạng với tam giác CDB (gg)
b)
vì ABCD hcn nên
AB=CD=12
BC=AD=9
AD Đlí pytado cho tam giác vuông CDB có
BD2=BC2+DC2
BD2=81+144
BD=15cm
theo câu a) ta có
AH/AB=BC/BD
=> AH= AB.BC chia BD
AH= 12.9 chia 15
AH= 7.2CM
C)
BD
CM
2 tháng 1 2019
Vì
△
AHB đồng dạng
△
BCD với tỉ số đồng dạng: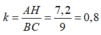 
Ta có: 
=
k
2
=
0
,
8
2
= 0,64 ⇒
S
A
H
B
=
0
,
64
.
S
B
C
D
S B C D = 1/2 BC.CD = 1/2 .12.9 = 54( c m 2 )
Vậy S A H B = 0 , 64 . S B C D = 0,64.54 = 34,56 ( c m 2 ).
TG
12 tháng 5 2021
a) Xét tam giác AHB và tam giác BCD ta có:
AHB = BCD (=90^0)
ABH = BDC (AB // CD và 2 góc slt)
=> Tam giác AHB đồng dạng với tam giác BCD (G-G)
b) Tam giác BCD vuonng tại C. Áp dụng Pitago ta tính được BD = 15cm
Tam giác AHB đồng dạng với tam giác BCD (G-G)
\(\Rightarrow\dfrac{AH}{BC}=\dfrac{AB}{BD}\Rightarrow\dfrac{AH}{9}=\dfrac{12}{15}\)
=> AH = 7,2 cm
c) Tam giác AHB vuông tại H. Áp dụng Pitago ta tính được HB = 9,6cm
\(S_{AHB}=\dfrac{1}{2}AH.HB=\dfrac{1}{2}.7,2.9,6=34,56\left(cm^2\right)\)