giúp mình làm và giải thích với. mình đag cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



3 raise money for sth: gây quỹ cho
4 be dependent on st/sb: phụ thuộc vào cái gì/ai
5 be treated for + bệnh: được điều trị bệnh gì
6 not believe a word of st: không tin 1 chút nào vào cái gì
7 the habit of + Ving: thói quen gì
8 be intent on sth: quyết tâm, dốc lòng phấn đấu
9 stand a chance of + Ving: có cơ hội làm gì
10 take (no) notice of sth: (không) chú ý đến cái gì
11 it's high time sb did st: đến lúc phải làm gì

1.in-at
2.at
3.at(ko chắc)
4.in-to
5.on
6.at
7.in(ko chắc)
8.in
9.in
10.at
11at-in
12.in

a)PQ \(\left\{{}\begin{matrix}quaP\left(1;-4\right)\\vtcp\overrightarrow{PQ}\left(1;7\right)\Rightarrow vtpt\overrightarrow{n}\left(7;-1\right)\end{matrix}\right.\)
\(\Rightarrow PQ:7x-y-11=0\)
b) Gọi pt đt tâm (O) có dạng (C):\(x^2+y^2=R^2\)
Do (C) tiếp xúc với đt \(2x+y-3=0\)
\(\Rightarrow R=d_{\left(O;\Delta\right)}=\dfrac{\left|2.0+0-3\right|}{\sqrt{2^2+1}}=\dfrac{3\sqrt{5}}{5}\)
\(\Rightarrow\left(C\right):x^2+y^2=\dfrac{9}{5}\)
c)\(I\in\left(\Delta\right)\Rightarrow I\left(t;3-2t\right)\)
\(IQ=R\Leftrightarrow\sqrt{\left(2-t\right)^2+4t^2}=3\)
\(\Rightarrow\left[{}\begin{matrix}t=\dfrac{2+\sqrt{29}}{5}\\t=\dfrac{2-\sqrt{29}}{5}\end{matrix}\right.\)\(\Rightarrow I\left(\dfrac{2+\sqrt{29}}{5};\dfrac{11-2\sqrt{29}}{5}\right);I\left(\dfrac{2-\sqrt{29}}{5};\dfrac{11+2\sqrt{29}}{5}\right)\)
Vậy pt đường tròn tâm I cần tìm là: \(\left(C\right)':\left(x-\dfrac{2+\sqrt{29}}{5}\right)^2+\left(y-\dfrac{11-2\sqrt{29}}{5}\right)^2=9\) hoặc \(\left(C\right)':\left(x-\dfrac{2-\sqrt{29}}{5}\right)^2+\left(y-\dfrac{11+2\sqrt{29}}{5}\right)^2=9\)
a.
\(\overrightarrow{PQ}=\left(1;7\right)\Rightarrow\) đường thẳng PQ nhận \(\left(7;-1\right)\) là 1 vtpt
Phương trình PQ:
\(7\left(x-2\right)-1\left(y-3\right)=0\Leftrightarrow7x-y-11=0\)
b.
Do đường tròn tiếp xúc denta nên \(R=d\left(O;\Delta\right)\)
\(\Rightarrow R=\dfrac{\left|2.0-0-3\right|}{\sqrt{2^2+1^2}}=\dfrac{3}{\sqrt{5}}\)
Phương trình đường tròn: \(x^2+y^2=\dfrac{9}{5}\)
c.
Do I thuộc denta nên tọa độ có dạng: \(I\left(a;3-2a\right)\)
\(\Rightarrow\overrightarrow{IQ}=\left(2-a;2a\right)\) \(\Rightarrow IQ^2=\left(2-a\right)^2+4a^2\)
Do đường tròn qua Q nên \(IQ=R\Rightarrow IQ^2=R^2\)
\(\Rightarrow\left(2-a\right)^2+4a^2=9\)
\(\Rightarrow5a^2-4a-5=0\Rightarrow\left[{}\begin{matrix}a=\dfrac{2+\sqrt{29}}{5}\\a=\dfrac{2-\sqrt{29}}{5}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}I\left(\dfrac{2+\sqrt{29}}{5};\dfrac{11-2\sqrt{29}}{5}\right)\\I\left(\dfrac{2-\sqrt{29}}{5};\dfrac{11+2\sqrt{29}}{5}\right)\end{matrix}\right.\)
Có 2 đường tròn thỏa mãn:
\(\left(x-\dfrac{2+\sqrt{29}}{5}\right)^2+\left(y-\dfrac{11-2\sqrt{29}}{5}\right)^2=9\)
\(\left(x-\dfrac{2-\sqrt{29}}{5}\right)^2+\left(y-\dfrac{11+2\sqrt{29}}{5}\right)^2=9\)

Part 1
1 on
2 as
3 who
4 so
5 well
6 didn't
Part 2
1 - G
2 - A
3 - F
4 - B
5 - C
6 - D
Part 3
1 have walked
2 learnt
3 watches
4 playing
5 be done
6 impressed
7 surprisingly
8 cosumption
Part4
1 reduce => reduces
2 whom => who


1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)


 Làm và giải thích, giúp mình nhanh nha mình cần gấp
Làm và giải thích, giúp mình nhanh nha mình cần gấp


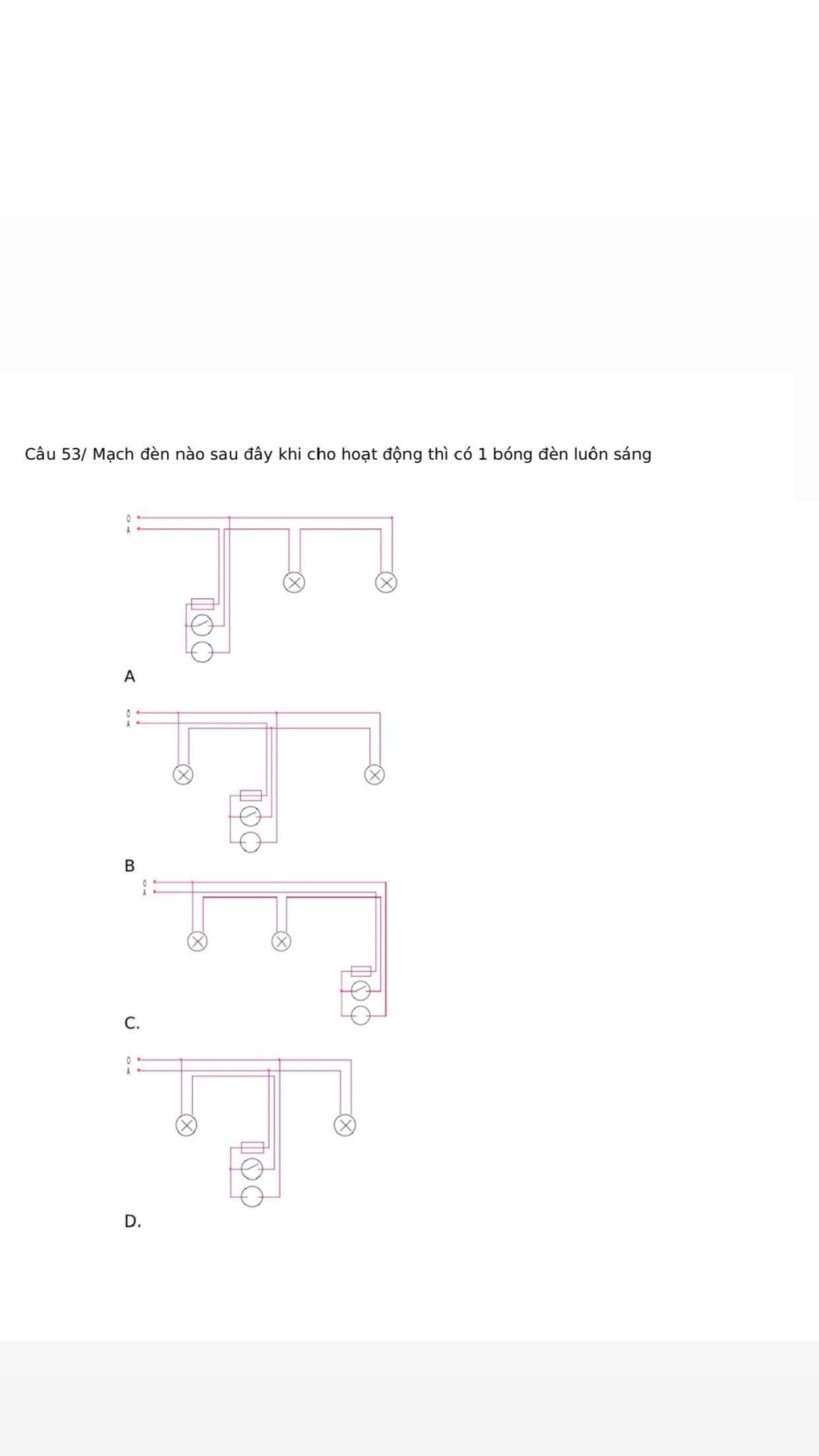 Giúp mình giải thích và đáp án với mình cần gấp !!!!
Giúp mình giải thích và đáp án với mình cần gấp !!!!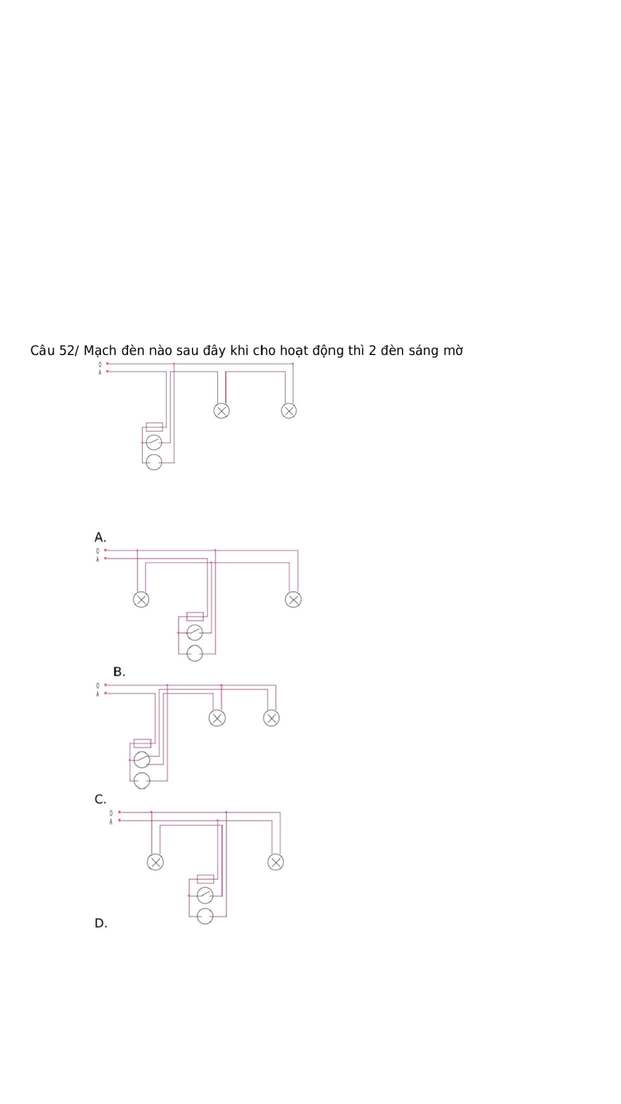

1 replaced
2 freezed
3 applicants
4 priceless
5 breakage
6 suspiciously
7 suited
8 beheaded
9 residential
10 outrageous